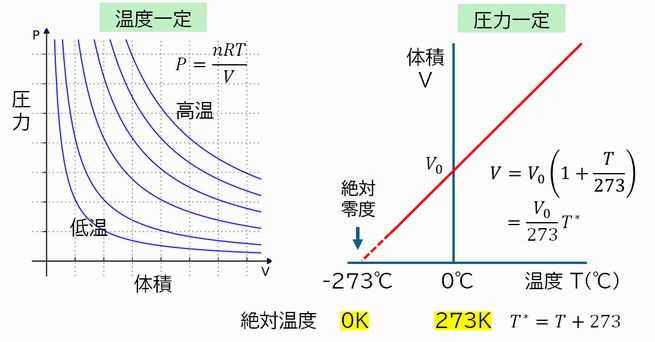
図3.1 ボイルの法則(左)、シャルルの法則(右)
前回の講義で熱エネルギーの話をしました。そのとき、普段の会話では、熱と温度を混同して使うことが多いが、物理学では明確に異なる概念であることを指摘しました。熱は 、より温度の高い 系から、より温度の低い系へ自発的に流れるエネルギーとして定義され、系の中にこれだけ熱が存在するというように定義できる物理量ではありません。これに対し て、温度は、それぞれの系において定義される量です。そこで、熱とは何か、温度とは何かについて今回は考えたいと思います。
まずは、温度について見ていきます。そのため、気体の性質について取り上げるのですが、3.1ではマクロな視点から、3.2ではミクロな視点から検討を行い、それぞ れの結果を突き合わせることから、温度とは何かを導き出します。これは、高校の物理で、気体運動論としてすでに学習した人もおられると思います。そうした方は 復習と思って読んでください。初めて出会う方は数式に戸惑うかもしれませんが、最終的に導かれた結論がこの後重要な意味をもつだけですので、導出の過程の詳細 が理解できなくても、どのような考え方で結論へと導かれたのかを、漠然とでもいいですので、理解するつもりで読んでいただければ結構です。
気体の状態は、その温度 \(T\) (Temperature)、体積 \(V\) (Volume)、圧力 \(P\) (Pressure) によって特徴づけることができます。この3つの量の間には、これから説明するボイル・シャルルの法則が成り立っています。これは、マクロな視点からの観察結果です。
温度が同じならば \(PV\) = 一定 すなわち (圧力)×(体積) = 一定 となります。これをボイルの法則といいます。一定量の気体をピストン付きシリンダーの中に入れ、ピストンを押して気体を圧縮して体積を小さくしていくことを考えます(図 3.1左)。 この とき、ピストンの内部と外部との間で熱の出し入れを可能にし、ピストンの周りを常に一定温度に保てば、ピストン内の気体の温度を一定に保つことができます(ただし、ゆっく り押 し込むことが必要です)。こうして、温度が一定の状態で体積を 1/2、1/3、1/4 に圧縮すると、圧力は2倍、3倍、4倍になるというのがボイルの法則の意味するところです。 これを、縦軸を圧力 \(P\)、横軸を体積 \(V\) としてグラフで表すと、図3.1左のような双曲線となります。これを \(PV\)曲線 とよぶことにします。温度により (圧力)×(体積) の値 が異なり、高温ほど原点から離れた双曲線となります。 後の講義でまた登場しますので、心に留めておいてください。

一方、圧力が一定ならば \(V/T\) = 一定 すなわち (体積)/(温度) = 一定 となります。これをシャルルの法則といいます。ただし、ここでいう温度は、ふだん使っている摂氏温度ではなく、この後説明する絶対温度とよばれるものです。今度は、体積 \(V\) を縦軸、温度 \(T\) を横軸にとると、(体積) = (定数)×(温度) ですので、図3.1右のように直線のグラフとなります。
この図では、摂氏温度 \(T\) を横軸、縦軸に体積 \(V\) をとり描かれています。極低温の実験値はありませんので、直線 をそのまま横軸まで外挿しています(直線の点線部分)。そして、その直線が、−273℃で横軸(温度軸)を横切ることを示しています。さらに直線を外挿していくと、体積 (縦軸)は負となります。負の体積は物理的にあり得ませんので、このことは、−273℃より低い温度は存在しない、すなわち温度には下限があることを示してい ます。そこで、この −273℃ を0度とする新たな目盛り、すなわち、 (摂氏温度) + 273 という目盛りの温度を定義します(目盛りの幅は自由に決められますが、摂氏温度と同じにします)。これを絶対温度とよび、単位は K(ケルビンと読みます)を使って表します。グラフでいえば、そこを原点とする座標に変換することに相当し、与えられた直線は原点を通る直線となります。このと き、直線の方程式は切片項がなくなるためすっきりして、その取扱いが簡便になるだろうというわけです。また、絶対温度ではマイナスの温度は存在しませ ん。これからは特にことわらない限り、温度はこの絶対温度で表すものとします。
ちなみに、絶対温度で表現すると、一定量の気体をピストン付きシリンダーの中に入れ、圧力を一定に保ちながら温度を上げていくと、温度が2倍、3倍、4倍 になったとき、体積が2倍、3倍、4倍になると表現することができます。すなわち、最初に掲げたシャルルの法則となります。 ボイルの法則とシャルルの法則をまとめると
\(PV = nRT\)
と書き表すことができます。これを気体の状態方程式とよびます。ここで \(n\) は気体の量で、モル数で表します。アボガドロ数 \(N_{A} = 6×10^{23}\) と同じ数の原子あるいは分子を含む系を1モルと定義します。また、\(R\) は比例係数で、気体定数とよばれます。この状態方程式は、温度 \(T\) と体積 \(V\) と圧力 \(P\) というマクロな(巨視的な)物理量の間に成り立つ関係式で、実験を通して得られたものです。
今度は、気体の温度 \(T\)、体積 \(V\)、圧力 \(P\) をミクロな(微視的な)視点から調べてみましょう。ボイル・シャルルの法則が目に見える世界の観察から得られた結果である のに対して、これから述べる内容は、目に見えない分子の世界を物理的に考察することから得られた理論的な結果です。途中、聞きなれない物理用語が出てくるかもしれません が、それをすべて丁寧に説明するととてもスペースが足りないので省略します。わからないところはそのまま読み進めて、話の流れだけ捉えていただければ結構で す。
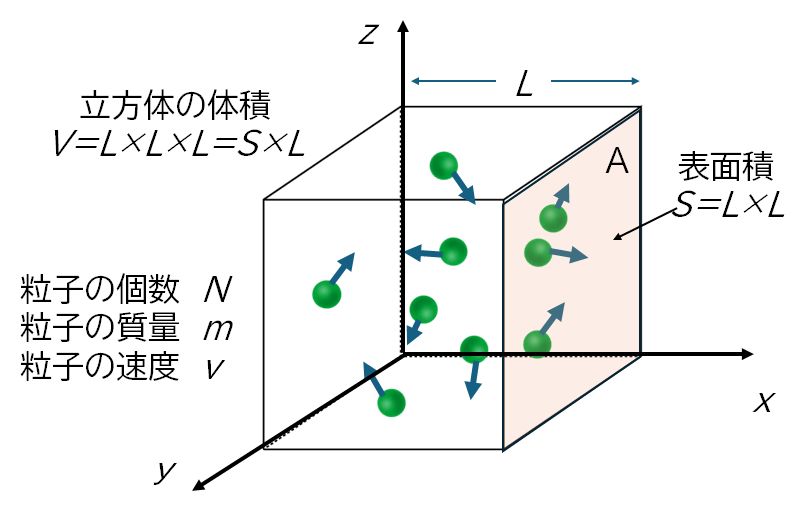
1辺の長さ \(L\) の立方体の容器内に質量 \(m\) の分子が \(N\) 個入っていて、容器内を飛びまわっているとします。図3.2のように座標軸を取り、いま、1個の分子が速度 \(v = (v_{x}, v_{y}, v_{z})\) で \(x\) 軸に垂直な面A に完全弾性衝突したとします。このとき分子1個の衝突で面A が受ける力積の大きさは \(2mv_{x}\) となります。
この分子は、時間 \(t\) の間に \(v_{x}t / 2L\) 回面Aと衝突しますので、面Aがこの分子から受ける時間 \(t\) の間の平均の力の大きさは \(f t = 2mv_{x} \times v_{x}t / 2L = mv_{x}^{2}t /L\)、すなわち \(f = mv_{x}^{2} /L\) となります。速度 \(v\) の2乗の平均値を <\(v^{2}\)> とすると、3平方の定理より <\(v^{2}\) > = <\( v_{x}^{2}\) > + <\( v_{y}^{2}\) > + <\( v_{z}^{2}\) > が、また、運動の等方性より < \(v_{x}^{2}\) > = < \(v_{y}^{2}\) > = < \(v_{z}^{2}\) > が成り立ちますので、<\(v^{2}\)> = 3 < \(v_{x}^{2}\) > あるいは < \(v_{x}^{2}\)> = (1/3) <\(v^{2}\)> となります。したがって、面Aが \(N\) 個の分子から受ける力の大きさ \(F\) は、\(F=Nf=Nmv_{x}^{2} / L = (1/3) Nmv^{2} / L \) となります。圧力は単位面積あたりの力で定義されますので、面A が受ける圧力は \(F\) を表面積 \(S\) で割って、 \( P=F/S\) \(=(1/3)Nmv^{2} / LS \) となります。ここで \(LS\) はこの立方体の体積 \(V\) に等しいので、結局、圧力は \( P=F/S\) \(=(1/3)Nmv^{2} / V \) あるいは \[PV = \frac{1}{3} Nmv^{2}\] となります。
こうして、分子の運動を考えることで、圧力 \(P\) と体積 \(V\) との関係を求めることができました。しかし、この式の中には温度 \(T\) が 含まれていません。
そこで、上のボイル・シャルルの法則から得られた状態方程式 \(PV = nRT\) と気体運動論から求めた方程式 \( PV= \frac{1}{3} Nmv^{2} \) を比較し てみましょう(定数 \(n\) はアボガドル数 \(N_{A}\) を使って \(N / N_{A}\) と表すことができます)。すると \( \frac{1}{3} Nmv^{2} = nRT = \frac{N}{N_{A}} RT \) が成り立つことが分かります。これを変形すると \[ T= \frac{2}{3} \frac{N_{A}}{R} \frac{1}{2} mv^{2} \] となります。すなわち、温度 \(T\) は、分子の平均の運動エネルギー \( \frac{1}{2} mv^{2}\) に比例するという結果が導かれたのです (運動エネルギーの式は、第2回の講義資料を参照してください)。温度が高いとは分子の運動エネルギーが大きいこと、温度が低いとは分子の運動エネルギーが小さいことと覚 えてください。
ところで、絶対温度では常に \(T \gt 0 \) で、\( T=0 \) に到達することはありませんので、\(v^{2} \gt 0 \) となります。すなわち、 \(T\) が 0 でない限り \(v\) も 0 ではないのです。この世のあらゆる物体は分子あるいは原子でできているわけですが、このことは、これら分子や原子は常に揺れ動いていることを意味します。 たとえば、気体では、互いにランダムな方向に飛び回っており、固体では、平均的な位置の周りで揺れ動いているのです。 マク ロに見ると静止しているように見える場合でも、ミクロの世界では常に、分子や原子は動いているのです。この運動を「熱運動」といいます。
(注) 熱運動という言葉は誤解を招くかもしれません。この資料の冒頭で、「熱はより温度の高い系から
より温度の低い系へ自発的に伝達されるエネルギーとして定義され、系の中にこれだけ熱が存在するという
ように定義できる物理量ではありません。」と述べ、さらに温度と熱を混同してはいけないと言いなが ら、
物体内部で起こっている分子の運動を熱運動というのに違和感があるかもしれません。むしろ温度が関わる
運動とでもいうべきかもしれません。しかし、慣例でそう呼んでいるので、これからもこの用語を使う こと にします。
上記の気体運動論の数式導出に戸惑った人も、具体的な現象に対して、定性的に熱運動と温度の関係につい て捉えておくことは今後の講義の展開では重要ですので、いくつか例をあげたいと思います。
ピストンは、エントロピーの説明ではしばしば登場する小道具です。すでに前回の講義の中で、仕事の計算例に登場しています。円筒形のシリンダー内に気体が入れられ、蓋に 相当する部分が可動で、その往復運動によって、あるいはそれを回転運動に変換することによって、さまざまな機械の動力として利用するも のです。このシステム全体をピストンとよぶこともありますが、本来は可動部分だけを指すようです。 しか し、この講義ではどちらの意味でも使うことがありますので、文脈から適宜判断していただければと思いま す。
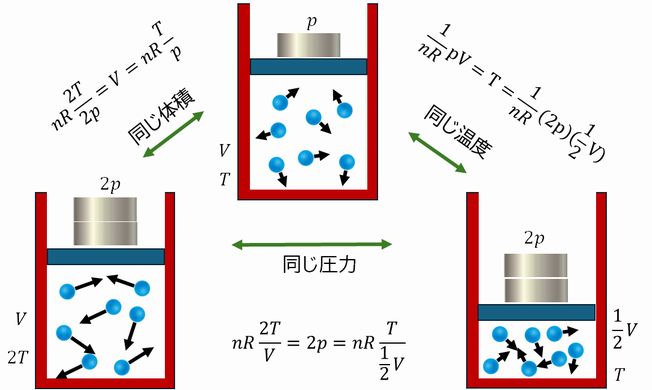
図3.3は、封入された気体の温度、したがって、その運動エネルギーとピストンの運動との関係を示したもの です。中央上の図では、シリンダーに乗ったおもりは一つです。しかし、外部から熱を加えるなどして温度が上がると、気体の運動エネルギーが大きくなり、より強く気体分子が ピストンを押すようになります。左下の図では、温度が倍になり、倍のおもりでも同じ体積を保っています。
一方、右下では、温度が中央上と同じです。すなわち、一つひとつの粒子の運動エネルギーは互いに同じです。しかし、体積が半分になったおかげで、分子がピ ストンに衝突する機会が倍になり、倍の重さに耐えることができています。
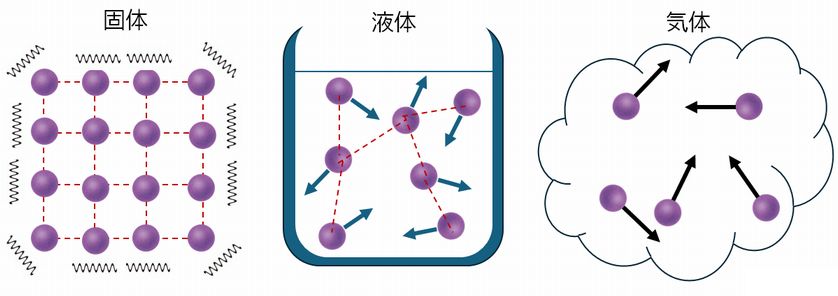
固体・液体・気体という物質の三態も熱運動という観点から見てみましょう。 温度が低いと熱運動の大きさは小さく、分子間の相互作用による束縛が打ち勝って秩序が保たれ、固体とな ります。このとき、マクロに見れば固体は静止していますが、その内部では原子や分子はその平衡点の周りで運動(振動)して いることになります。温度が上がり、構成分子の熱運動が大きくなると、ある程度束縛は受けるものの、か なり自由に動けるようになったのが液体、そしてさらに温度が上がって、束縛を完全に断ち切って自由に運動しているのが気体となります。
熱は、ある系からある系へと伝わるエネルギーとして定義されることを強調してきました。したがって、 その伝わり方を見ておくことは重要です。何か難しそうな言い回しですが、要するに熱の伝わり方のこと で、伝導、輻射、対流の3つがあることは理科で習う初歩的なことと思います。ここでは、熱運動の視点からこれらを確認しておこうと思います。
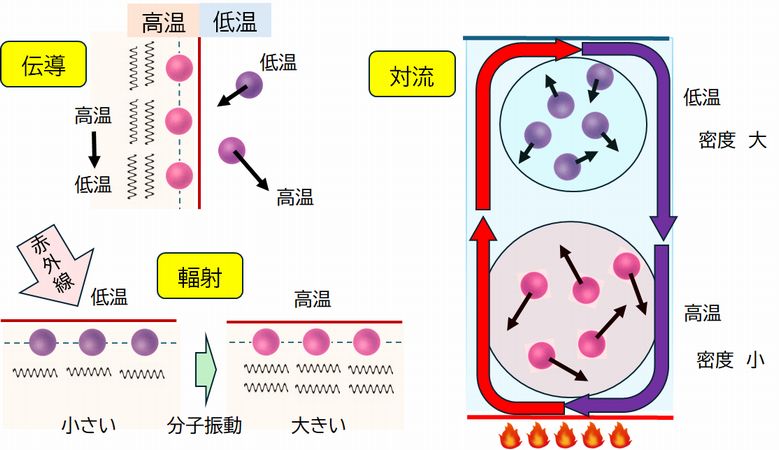
(1) 伝導 温度が異なる2つの物体が接触した場合、接触面を介して高温側から低温側に熱が伝わります。これを熱 の伝導といいます。このとき、接触面では、両者の分子どうしがぶつかり合います。温度の高い側の運動 エネ ルギーの大きい分子が温度の低い側の運動エネルギーの小さい分子と衝突することで、前者は運動エネル ギーを少し失い、後者はその分運動エネルギーが増加します(エネルギーは保存されますから、一方のエネルギーが減少すれば、必ずもう一方のエネルギーがその減少分だけ増加 します)。このことは、両者の温度の差がなくなるまで、すなわち、等しい温度になるまで続きます。
(2) 輻射 分子は絶えず運動していますが、その運動の結果、分子の種類とそのときの温度によって決まる電磁波を 放出します。通常の部屋の温度や体温では、その主成分は赤外線です。一方、その赤外線を受けた物体の分 子もそれを吸収し運動が大きくなります。すなわち温度が上がります。こうして熱が伝わるわけで、これを輻射熱といいます。 太陽光は真空である宇宙空間を進んできますから、分子どうしの衝突である伝導では熱を伝えることができ ません。しかし、この輻射熱の形でわれわれを温めてくれます。また、冬の晴れた夜間、あるいはそれが明け た朝、放射冷却によって冷え込むことがありますが、この放射冷却も、地上から宇宙空間へ赤外線を放出す るため、地面の温度が低くなることで起こる現象です。曇っていると、雲がその放射を妨げ、放射冷却を抑えてくれます。 また、物体(生体も含む)から放射される赤外線のエネルギー量を赤外線センサーで検知し、物体の温度を測定 するのが赤外線放射温度計(赤外線サーモグラフィー)です。
(3) 対流 熱せられた流体が上部へ移動し、低温の流体が下降するといった流体 (分子の集合体)の移動を対流とよびますが、こうした流体の移動に伴なう熱の伝わり方もあります。ちなみに、下部では温度が高くなると分子の運動が大きくなり、それらが占 める体積が大きくなります。結果、単位体積当たりの質量、すなわち密度が小さくなり、軽くなるため、上部へと移動することになるわけです。
この3つの熱の伝わり方は、この講義の今後の話題の中で幾度となく取り上げられる重要な現象ですので、心に留めておいてください。
拡散とは、分子や粒子や熱などが、散らばり、広がっていく現象です。角砂糖を水に入れると、かき混ぜ なくても溶けて、時間さえかければ、やがて一様な濃度の砂糖水となります。タバコの煙や汚染物質も、風がなく ても空気中や澄んだ水の中へと広がっていきます。冷たいものと温かいものが接触した場合、熱が温かいも のから冷たいものへと流れ、やがてすべてが均一の温度となります。これらすべて拡散現象ですが、これら は外力がなくても起こります。それは構成する分子が熱運動しているからです。
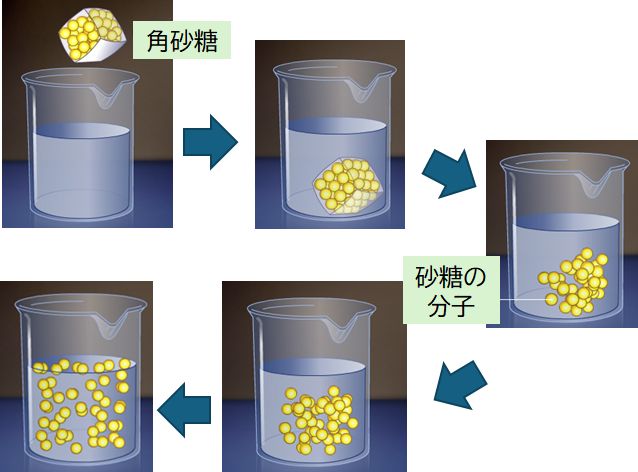
ここで重要なポイントがあります。砂糖の分子も水の分子も、互いに強い相互作用がない場合、分子はそ れぞれ勝手に動きまわります。だからこそ、拡散し、お互いに混じり合うのです。しかし、そうした状態で ランダムに運動する砂糖の分子がすべてもう一度集まって、角砂糖の形になることは確率的にありえませ ん。これこそが現象の不可逆性です。この点については、次回、もう一度触れたいと思います。
今回の講義をまとめましょう。
・温度には下限 (−273℃) があり、そこを 0 として測るのが絶対温度です。ただし、絶対温度の
0K(絶対零度といいます)には到達することはできず、常に正の値をもちます。
・物体の温度とは構成する分子の運動エネルギーに比例する量です。
・これらのことから、すべての物体の内部では、マクロにいかに静止しているように見えたとしても、ミク
ロに見れば、分子は運動していることになります。これを分子の「熱運動」とよびます。
このことが、エントロピーの本質をなしていることが、後にわかると思います。
⇒ 第4回 混合
