 �@�@�@
�@�@�@
�}4.1�D�S�̐L�яk�݂������邽�߂̃��f��
�@�O��̍u�`�ŁA�����̐g�̉��ɂ�����̂͂��ׂāA�����ځA���Ȃ킿�}�N���ɂ͓����Ă��Ȃ��Ƃ��A�����̃~�N���̐��E�ł́A���q�������M�^�����Ă��� ���Ƃ��q�ׂ܂� ���B�������A����ł͂Ȃ��A�����ړ����Ȃ��̂ł��傤���H���ꂪ�����̍ŏ��̃e�[�}�ł��B
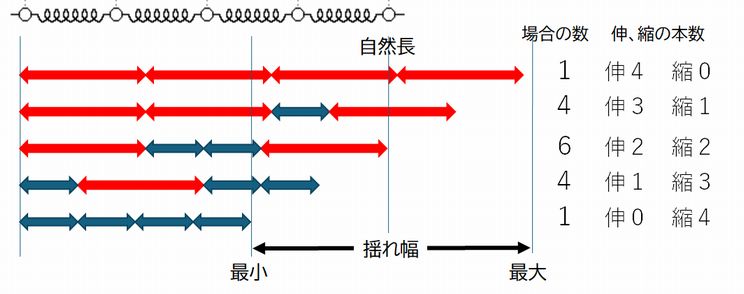
�@�����ŁA�ȒP�ȃ��f�����l���A���ׂĂ݂܂��傤�B�ő̂̓S�̉���l���܂��B�}4.1�̂悤�Ƀ~�N���Ɍ���ƁA�S�̌��q�́A�݂��̑��ݍ�p�ɂ���čœK�ȋ��������邽�� �i��2��u�`�̌��q�Ԃ̃|�e���V�����G�l���M�[�Q�Ɓj�A���̋�����ۂ��Đ��R�ƕ���ł��܂��B����A�O��̍u�`�ŁA���q�͂��ׂĉ^�����Ă���Ƃ������Ƃł��� �� ��A���q�͂��݂��̑��ݍ�p�ɑ�������Ȃ�����A���̍œK������菭�����ꂽ��A�߂Â����肵�Ȃ��烉���_���ɐU�����Ă��܂��B�}4.1���͂��̗l�q��͎��I�ɕ`�������� �ł��B �e�������q��\���A���q�Ԃ̑��ݍ�p���o�l�ŕ\�����Ă��܂��B3�����ōl����͖̂ʓ|�Ȃ̂ŁA�}4.1�E�̂悤�ɉ�1��݂̂��l���܂��B���q�̓����ɒ��ڂ��� �������ł����A�o�l�̐L�яk�݂Ƃ��Č��q�̉^���𑨂��邱�Ƃ��ł��܂��B�������A����Ƀ��f�����ȗ������āA�o�l�́A�L�т���ԁi�Ԃ̖��j�Ək��ԁi�� �̖��j��2�� ��Ԃ̂ǂ��炩�����Ƃ�Ȃ��Ƃ��܂��B�����āA���ꂼ��̃o�l�͑��̃o�l�Ƃ͊W�Ȃ��A�L�т���k�肷��Ƒz�肵�܂��B����ƁA���R�A�L�т���Ԃ̃o�l���� �|�I�ɑ�����A�}�N���ɂ��S�̉�͐L�сA���R�A�k��Ԃ̃o�l�����|�I�ɑ�����A�}�N���ɂ��S�̉�͏k�ނ͂��ł��B��͂�A�S�̉�́A�}�N���Ɍ��Ă��A �L �т���k�肷��̂��{���̎p�ł͂Ȃ��ł��傤���H
 �@�@�@
�@�@�@
�}4.1�D�S�̐L�яk�݂������邽�߂̃��f��
�@�������A�����ōl����ׂ��_������܂��B���ꂼ��̃o�l�͑��̃o�l�Ƃ͖��W�ɐL�т���k�肷��ƁA�}4.1�E�̗�ł͂S�{�̃o�l������܂�����A�S ���� \( 2^{4}= 16 \) �ʂ�̏ꍇ������܂��B�����̂����A�S�����L�т���ԂƑS�����k��Ԃ͂Ƃ��ɂP�ʂ肵���Ȃ��̂ɑ��āA���Ƃ��A�Q�͐L�т���ԂŎc��̂Q�͏k��ԂƂ��� �̂́A �g�ݍ��킹�̖��ł����A\( _{4} \mathrm{�b}_{2} = 6 \) �ʂ肠��܂��B���̂U�̏ꍇ�́A�S�̂̒����͑S�����L�т���ԂƑS�����k��Ԃ̒��ԂƂȂ�A�ǂ�����������ɂȂ�܂��B���Ȃ킿�A�X�̃o �l���ǂ���̏�Ԃɂ��邩�Ƃ��������I�ȏ�ԂɈႢ�������Ă��A�����͂����F�����邱�Ƃ��ł��܂���A�S�̂̒����Ƃ��������I�ȗʂ����ɒ��ڂ���ƁA����6�� �ꍇ�ɂ��Ă͈� �����Ȃ��A������ԂƔF�������킯�ł��B���ǁA�S�̂̒����͂��낢��ω����邱�Ƃ��\�ł����A���̒����ɂ���ďo���m�����قȂ�Ƃ��������܂�邱�ƂɂȂ�� ���i�}4.1�E�̉E�[�̐��������̏ꍇ�̐��������Ă��܂��j�B�������A�ǂ̒������o���m���� 0 �ł͂Ȃ��킯�ł�����A��͂�A�S�̂̒������ω����Ȃ��Ƃ��������ɂ͂Ȃ��Ă��܂���B
�@�����ōX�ɁA���̏o���m���̃o�l�̖{���i���Ȃ킿�A�\�����錴�q�̐��j�ւ̈ˑ����ׂĂ݂܂��傤�B���܃o�l�̑��{���� \(n\) �{�Ƃ��܂��B�S�̂̒��� \(L\) �͌Œ肵�A 1�{�̃o�l�̒����� \(L/n\) �Ƃ��܂��B���������1�{1�{�̃o�l�̒����͕ω����܂����A���ꂼ��L�т���ԂƏk��Ԃ͎��R�Ȓ����́A���Ƃ���10%�������� �� 10%���Ƃ���ƁA���ׂẴo�l���L�т���Ԃ̂Ƃ��̒����ƁA���ׂẴo�l���k��Ԃ̂Ƃ��̒����̓o�l�̖{���ɂ͈ˑ������A���ꂼ�� \(1.1L\)�A\(0.9L\) �ƂȂ�܂��B���� \(n\) �{�̃o�l�̂��� \(r\) �{���L�т���ԂƂ���ƁA���̏ꍇ�̐��� \( _{n} \mathrm{C}_{r} \) �ƂȂ�܂��B���������āA�S�̂̒���������l���Ƃ�m���� \( _{n} \mathrm{C}_{r} \) �ɔ�Ⴕ�܂��� �ŁA \( _{n} \mathrm{C}_{r} \) �� \(r\) �ɂ��ăv���b�g������낢��Ȓ����̏o���m�����킩�邱�ƂɂȂ�܂��B
�@�}4.2�Ƀo�l�̖{����6�A60�A300�̏ꍇ�ɂ��Ă��̊m�������߂����ʂ������܂����B
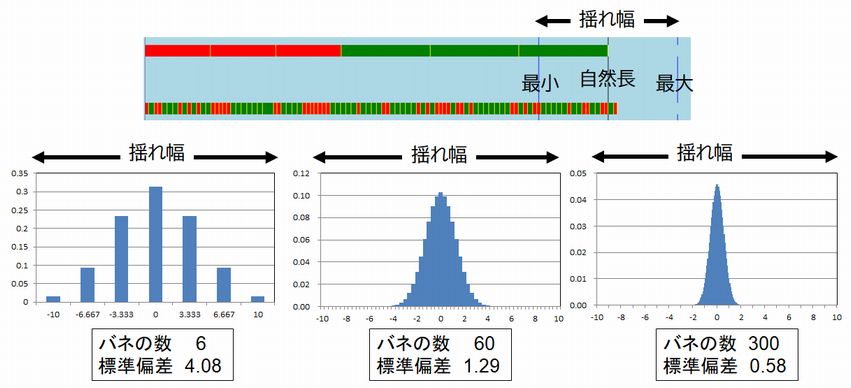
�@�E�[�����ׂẴo�l���L�т���� \(1.1L\)�A���[�����ׂẴo�l���k��� \(0.9L\) �ŁA���������̒��Ԃ̒l�i���ϒl�j\(L\) �ƂȂ�܂��B���v�w����������͂������������������킩�������Ǝv���܂��B�o�l�̖{�����ς�邱�ƂŊm���̕��z ���ς��̂ł��B�o�l�̖{����������Ɗm���̍L����A���Ȃ킿�W�������������Ȃ�̂ł��i \( \sqrt{n} \) �ɔ���Ⴕ�ď������Ȃ�܂��j�B ���ۂ̌��q�̐� \(n\) �̌����� \(10^{23}\) �ł��B���ϒl����̂���A���Ȃ킿�W�����͂���߂ď������Ȃ�A�����ڂ̒����� \(L\) ��蒷���Ȃ�����A�Z���Ȃ����肷��m���͎��� 0 �ƂȂ�܂��B���������āA���������ŔM�^�����N�����Ă��Ă��A����炪�����_���ɋN�����Ă���̂ł���A�����I�ʂ͕ω����Ȃ��Ƃ������ƂɂȂ�܂��B�����_�����Ƃ͕� ���Ȃ����Ƃł�����A�E�ɓ������̂�����A����Ɠ������������ɓ������̂�����A��ɓ������̂�����A����Ɠ������������ɓ������̂�����̂ł��B�ǂ�� �����ł� �낤�ƁA���铮���Ƃ��̋t�̓��������錴�q���邢�͕��q�̐��͂قړ����ł���A���̍��́A�S�̂̌��q���╪�q���Ɣ�ׂ���A����Ȃ��������Ƃ�����̂ł��B
�i���j�u�m�� \(p\) �ŋN���鎖�ۂɂ��āC ���s�� \(n\) ��s�����Ƃ��C ���̎��ۂ��N������ \(r\) ��ł������Ƃ���B���̂Ƃ��C���s�� \(n\) ���傫���Ȃ�Ȃ�قǔ䗦 \(r / n\) �́A \(p\) �Ɍ���Ȃ��߂Â��Ă����v�Ƃ������v�w�̑吔�̖@�����A�����ł͒P�ɏq�ׂĂ���ɂ����܂���B�R�C����10���A6��\�ŁA4�ł��s�v�c�Ɏv���܂��i5��A5�� �Ƃ������_�I�ȕ��ϒl���炸���m���͂���܂����j�A1�����A6�疜��\�ŁA4�疜�Ƃ����f�[�^�������炨�������Ǝv���i5�疜��Ƃ������_�I�ȕ��� �l ���炱��Ȃɂ������m���͂قƂ�� 0 �̂͂����j�A����Ȓ����ŗ������Ă���������Ό��\�ł��B
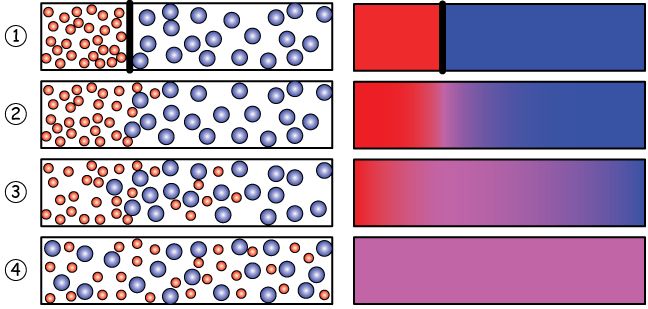
�@�O��̍u�`�Ŋg�U�̘b�����܂������A�����I�ȏ�Ԑ��𐔂���Ƃ����ϓ_���������x���Ă݂܂��傤�B
�@�}4.3�ɊȒP�ȃ��f���������܂����B
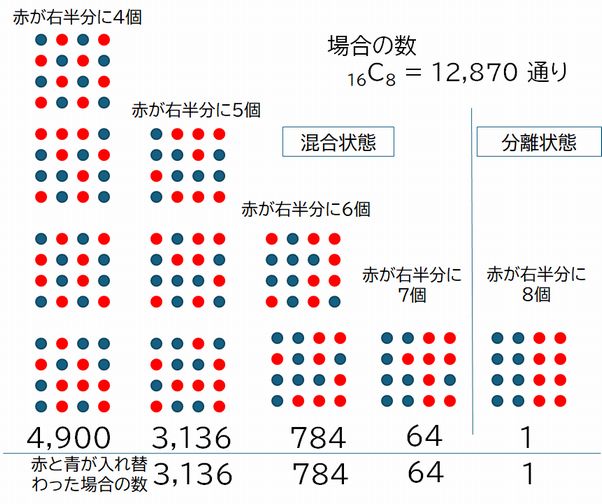
�@������16�̕��q����Ȃ�n�ł��B�ԐF�̕��q��8�A�F�̕��q��8�ł��B����炪���R�ɓ����Ă����̂ł����A�ȒP�ɂ��� ���߂Ɋi�q�_�̏�ɂ̂ݑ��݂���Ƃ��Ă��܂��B�����w�ł́A�悭�A�������Č�������ɒP�������čl���܂��B ���āA�Ԃ̕��q�Ɛ̕��q�̔z�u�̎d���͉��ʂ肠�邩�ƌ����ƁA16�i�q�_�̒�����8�̊i�q�_��I��ŐԂƂ���A�c�肪�Ƃ������ƂɂȂ�܂�����A \( _{16} \mathrm{�b}_{8} = 12,870\) �ʂ肠��܂��B���̂����A�Ԃ��E�����A���������ƂȂ�̂�1�ʂ�ł���̂ɑ��āA�Ԃ�4�E�����ɁA�c���4���������ɂ���̂�4,900�ʂ肠��� ���B���̑��̏ꍇ�̐��͐}4.3�̒ʂ�ł����A�����Ŗ��ƂȂ�̂́A����ꂪ�ԂƐ��������Ă���Ƃ��A������Ԃɂ���Ƃ��\������Ƃ��A���������I�� �Ԃ̂ǂ�ɑΉ����邩�Ƃ������Ƃł��B���̐��m�ȋ��E�͋c�_�����邩������܂��A��Ȃ��Ƃ́A������Ԃɕ��ނ��������I��Ԃ����|�I�������߂�Ƃ� ���_�ł��B�����ĕ��q����������A������Ԃɕ��ނ��������I��Ԃ̊����͌���Ȃ� 0 �ɋ߂��Ȃ�Ƃ������Ƃł��B
�@���q�͎��R�C�܂܂ɓ����Ă��܂��܂Ȕ����I��Ԃ��o����܂��B�ǂ̔����I��Ԃ����m���Ŏ��������ƍl���邱�Ƃ��ł��܂��B�������A�����I��ԂƂ��Ă�� ��� ���ώ@����Ƃ��ɂ́A�X�̔����I��Ԃ́A���Ƃ��Ε�����Ԃ�������Ԃ̂ǂ��炩�ɕ��ނ���Ă��܂��܂��B�����Ȃ�ƁA���̔����I�� �Ԑ��̑��������I��Ԃ��m���I�Ɏ�������₷���Ƃ������ƂȂ�܂��B�����āA����̋����I��Ԃ̔����I��Ԑ������|�I�ɑ����ꍇ�ɂ́A���Ƃ�������Ԃ͔����I��Ԑ��̏��� �������I��Ԃɂ������Ƃ��Ă��A�n�͎���ɔ����I��Ԑ��̑��������I��ԂւƑJ�ڂ��A�Ăє����I��Ԑ��̏��Ȃ������I��Ԃɖ߂邱�Ƃ͂قƂ�ǂ��蓾�Ȃ��A�� �Ȃ킿�A�����I�ɁA���̊m���� 0 �ƂȂ�܂��B���ꂪ�A�����I��� ���Ƃ����ϓ_����݂������I���ۂ̕s�t���ł���A���́A���ꂱ�����A�G���g���s�[����̖@���������Ƃ��Ă��邱�ƂȂ̂ł��B
�@�����ɒu�������ԁB�����J���A�����������ނƕ��Ԃ����܂��B�������A����߁A�����̋�C�ɓ������Ȃ��Ȃ�ƁA���Ԃ͎~�܂��Ă��܂��܂��B�Ȃ��ł��傤���H�� ���A�����J���Ă����Ƃ����Ԃ��Ă�����C�͂ǂ��Ȃ��Ă��܂����̂ł��傤���H����Ȗ����l���Ă݂����Ǝv���܂��B
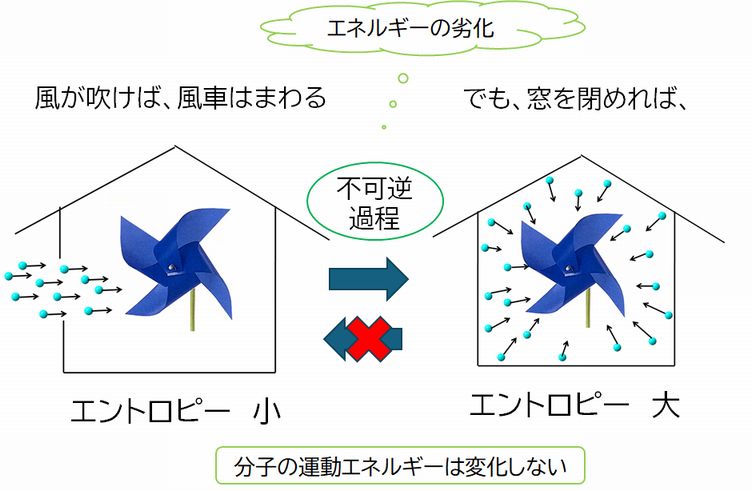
�@���͋�C�̕��q�������ē��������ɉ^�����Ă����ԂƂ����܂��i�}4.5���j�B���̕��q�����́A�����������ɉ^�����Ȃ��畗�ԂɏՓ˂��邱�Ƃŕ��Ԃ����Ƃ��ł� �܂��B�������A����߂�ƁA�����ĉ^�����Ă�����C�̕��q�����͂��̌�A�����̕ǂ₳�܂��܂ȕ��ɏՓ˂��A���̌�����ς��Ă����܂��B���̊ԁA���ۂɂ͏Փ� ���� ���Ƃŕǂ╨�����߁A�G�l���M�[�������܂����A�Ƃ肠�������������A��C�̂��^���G�l���M�[�̑傫���͕ς��܂���i�G�l���M�[�ۑ��̖@���j�B�����A�^���̕��� ���� ���ɂȂ��Ă��܂������Ƃɂ��A��C�̕��q�����͍Ăѕ��ԂɏՓ˂���Ƃ��ɂ́A���܂��܂ȕ�������Փ˂���悤�ɂȂ�܂��B���̐��͖c��ł�����A�����������Փ˂� �� ���q�̐��� ���̕������傫���Ȃ�m���͂قƂ�� 0 �ƂȂ�܂��B���̂��߁A���ԂɏՓ˂��Ă��镪�q�̗͂��݂��ɒނ荇���A���Ԃ��͂Ƃ͂Ȃ蓾�Ȃ��̂ł��B���Ƃ��Ċϑ�����Ă��� ��C�̕��q�����́A���ς�炸�����傫���̉^���G�l���M�[��ێ����Ă���̂ɁA�^�������������_���ɂȂ������ƂŁA���Ԃ��Ƃ����d�������邱�Ƃ��ł��Ȃ� �Ȃ����̂ł��B
�@��2��u�`�̃G�l���M�[�ۑ��̖@���̘b��̂Ƃ��A�G�l���M�[�̗ʂ͑�������������Ȃ��̂ɁA�Ȃ��ߖȂ�������Ȃ�����₢�܂����B����ɑ��āA �u�ʂ͕ۑ����� �邪�A�G�l���M�[�̎��͗���v�Ɠ����邱�Ƃ��ł��܂��B���͕��q�������ĉ^�����Ă��܂��B�Â��ȕ����ł���C�̕��q�͉^�����Ă��܂��B�������A���ꂼ�ꂪ�o���o���� �����ɉ^�����Ă���ƕ��Ԃ����Ƃ��ł��܂���B���̃o���o���ɂȂ������Ƃ��G�l���M�[�̎��̗̓T�^��Ȃ̂ł��B �������A�o���o���ɉ^�����Ă����C�̕��q���ЂƂ�łɂ݂�ȑ����ĉ^������悤�ɂȂ邱�Ƃ͐�ɂ���܂���B�����Ă�����̂��o���o���ɂȂ邱�Ƃ͋N����܂����A���� �t�͋N����Ȃ��B���������āA������s�t�������������ۂ̗�ƂȂ�܂��B��C�̕��q�������ĉ^�����A���Ԃ��Ƃ�����Ԃ̔����I��Ԑ��ƁA����炪��� ��� �^�������Ԃ����Ƃ��ł��Ȃ��Ƃ�����Ԃ̔����I��Ԑ��ł́A��҂����|�I�ɑ傫�����߂ɁA���������ƂȂ�̂ł��B�����Ă�����܂��A�G���g���s�[����̖@���� ����������ۂƂ������ƂɂȂ�܂��B
�@�Ƃ���ŁA��@���g���Ε��𐁂������Ƃ͂ł����Ȃ��̂��A�Ǝv��ꂽ����������Ǝv���܂��B�m���ɂ��̒ʂ�ł��B�O������̃G�l���M�[���g���A�Ă� ���𐁂������Ƃ��\�ł��B����Ȃ牽�����ɂȂ�Ȃ��̂ł́A�ƌ��������Ƃ���ł����A�u�G�l���M�[���g���v��ŏq�ׂ��u�G�l���M�[�̗v���K������ �Ȃ�� ���B���Ԃ����ƂŐ��ݏo����闘�p�\�ȃG�l���M�[�i���̏ꍇ�A���Ƃ��Γd�C�G�l���M�[�j�ƁA��@�����ƂŐ�����G�l���M�[�̗�V���ɂ������Ƃ��A �ǂ��炪�D���Ȃ̂��Ƃ��������́A�����܂ł̋c�_�ł͉��Ƃ������܂���B���̖��ɓ����邽�߂ɂ͂������炭�������K�v�ł��B
�i���Ԃ��Ĕ��d���A���̓d�C���g���Đ�@���܂킵�A����ŕ��Ԃ��Ĕ��d���E�E�E�B���āA �����N���邩���l���Ă݂Ă��������B�j
�@�S�̐L�яk�݂�����ꂪ�ϑ��ł��Ȃ��̂́A���ɑ����̐��̕��q����Ȃ邽�߁A���ϒl����̕��U���邢�͕��ϒl�̂܂��̗h�炬�����ɏ��������߂ł� ��Ə�Ő������܂����B�������t�ɁA�ւ�镪�q�̐������Ȃ���A�����͋����I�Ȍ��ۂł��h�炬�i���ϒl����̂���j���ϑ��ł��邱�Ƃ��������Ă���Ƃ� �����܂��B �������A���q�╪�q�ڌ��邱�Ƃ��ł���A���������h�炬���ϑ��ł���͂��ł����A�������������I�Ȑ��E�ŁA�h�炬���ϑ����邱�Ƃ͂ł��Ȃ��ł��傤 ���B���́A���w�������Ō�������x�̐��E�ŁA���̗h�炬���ϑ��ł��錻�ۂ�����̂ł��B���ꂪ�A�u���E���^���Ƃ�����̂ł��B
�@�u���E���^���́A���Ƃ���1827�N�A�A���w�҃��o�[�g�E�u���E�����ԕ����������Ŋώ@���Ă����Ƃ��A���̐Z�����Ŕj���ԕ����琅���ɗ��o�����V���������q �������_���ɓ����Ă��邱�Ƃ��������ƂɗR�����܂��B�����A���̔����q�������������Ƃɂ��^���ƍl�����܂������A���̌�A�����̔����q�Ȃǂł����� �� �ۂ��N���邱�Ƃ���A�����Ƃ͊W�̂Ȃ����ۂƂ킩��܂��B���݂ł͈�ʂɁA�t�̂̂悤�ȗn�}���ɕ��V��������q�������_���ɉ^�����錻�ۂ��u���E���^���Ƃ��ł��� ���B
�@���̌��ۂ̌����͒����ԕs���̂܂܂ł������A1905�N�A�A�C���V���^�C���ɂ��A�M�^������}���̕��q�̕s�K���ȏՓ˂ɂ���Ĉ����N������Ă���Ƃ����_���� ���\����܂����B���̘_���ɂ��A�����܂��s�m�����������q����ѕ��q�̑��݂������I�ɏؖ��o����\����������܂����B��ɂ���͎����I�Ɍ�����A���q�� �� �q���m���Ɏ��݂��邱�Ƃ��m�F���ꂽ�̂ł��B
 �@�@�@
�@�@�@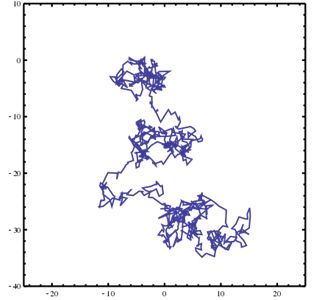
�@�u���E���^���ł́A�ԕ������яo�������q���炢�̑傫���̂��̂ɑ����̐����q���Փ˂���킯�ł����A������ƉE����A���邢�͏ォ��Ɖ�����A�Ƃ������t���� �ŏՓ˂��Ă��镪�q�̐��ɗL�ӂȂ�����o�邽�߂ɗ��҂̏Փ˂��ނ荇�킸�A�����Ɨh�炢�ł��܂��̂ł��B
�@�����̐g�̉��ɂ�����̂́A�c��Ȑ��̌��q�╪�q����ł��Ă��܂��B�������A��~���Â��镪�q�͈���Ȃ��A��Ή��x�ɔ�Ⴗ��^���G�l���M�[�� �����ĉ^�����Ă��܂��B �ނ�́A���q�Ԃ̑��ݍ�p�ɂ���Ă�����x�����͎܂����A�����_���ɉ^������]�n�͏�Ɏc����Ă��܂��B���������̒��ł́A���Ƃ��A�R�C����10�� �����ɓ����đS���\���o��Ƃ������Ƃ́A1000�������1�x���炢�N����܂����A1���������ɓ����đS�����\�ɂȂ邱�Ƃ͋N���蓾�Ȃ��悤�ɁA����番�q ���� ���A�O�����牽�炩�̎�������邱�ƂȂ��A���炩�̒�������U����������m���͎��� 0 �ƂȂ�܂��B���������āA�O������̑���ʼn��炩�̒�������U���������Ă����� ���Ă��A���̑������߂�A�Ђ����疳������ԂւƑJ�ڂ��Ă����A�Ƃ������Ƃ��C���[�W�ł����ł��傤���B�܂��G���g���s�[���`���Ă��܂��A���ꂱ�����A �G���g���s�[����̖@���Ȃ̂ł��B
�@�����āA�����_��������Ƃ́A�肪�Ȃ��Ȃ�����ւƕω�����Ƃ������Ƃł�����܂��B���炩�̍��������A�ψꉻ���Ă����Ƃ������Ƃł��B�M�����̂Ɨ₽ �����̂�����A�ڐG������A���̉��x������������悤�Ɉ�l�ȉ��x�ɂȂ��Ă����܂��B�g�U�͔Z�x������������ω��Ƒ����邱�Ƃ��ł��܂��B���C���ƒ�C���� ���͍��� ����āA���������A���ꂪ���܂��܂ȋC�ی��ۂ������N�����܂����A��������͍����������邽�߂̕ω��Ƒ����邱�Ƃ��ł��܂��B�����Ă��̍�����������A�ψ�ɂȂ�ƁA �ω��͎~�܂�܂��B���ꂪ�G���g���s�[���ő�ɂȂ�����Ԃł��B �����ł��В��ڂ��Ă����Ăق����_�́A�G���g���s�[����̖@���́A��������Ƃ��A�����������邽�߂ɗ�����A�������������Ƃ��̗���͏�����Ƃ������Ƃ��� �����܂��B����������ŁA���C���E��C���̗�̂悤�ɁA��[�����Ă��܂����̍��ݏo���@�\�����R�E�ɂ͂��肻�����Ƃ������Ƃ��S�ɗ��߂Ă����Ă��������B ����͂��̍u�`�̍Ō�̕��ŁA�ƂĂ��d�v�Ȏ��_�ƂȂ�܂��B
�ˁ@��5��@�M�@��
