�@�G���g���s�[����̖@���͕��ՓI�ɐ��藧�@���ł��B����������������ƁA�G���g���s�[�̑���̖@���ɔ�����悤�Ɍ����錻�ۂ����X����܂��B�P���Ȏ� ������זE������J��Ԃ��Ȃ��畡�G�Ȑ��̂��g�D������܂��B�����̓��X�̉c�݂��A��{�A�P�퐫���ۂ���Ă���A���X�A�̓��̃G���g���s�[�����債�Ă� �� �Ƃ͂ƂĂ��v���܂���B�i���̉ߒ����A�����_�����𑝂��ǂ��납�A��蕡�G�ȁA��荂���Ȑ����̂ݏo���Ă��܂����B�{���ɃG���g���s�[����̖@���͕��ՓI �ɐ��藧�̂ł��傤���B����Ƃ��A���������������w�ōl���Ă͂����Ȃ��̂ł��傤���B
�@���������^��ɓ����邽�߁A����x�A�G���g���s�[����̖@���̏ؖ��ߒ����v���o���Ă݂܂��傤�B�J���m�[�T�C�N�����g���Ă��낢��ȏؖ�����
�܂������A��ɁA�O������d�����s�����ƂȂ��A�ቷ�����獂�����ɔM�����R�ɗ���邱�Ƃ͂ł��Ȃ�����A�Ƃ����̂��Ō�̌��ߕ���ł����B�N���E�W�E�X�̌�����
�����邩��A�Ƃ��\������܂����B�ł́A�{���ɒቷ�����獂�����ɔM�͎��R�ɗ���Ȃ��̂ł��傤���B����̓G���g���s�[����̖@���ɔ����邩��A�Ƃ����̂͗�
�R�ɂ�
��Ȃ����Ƃ��������܂����B�m���ɁA�G���g���s�[����̖@����F�߂���̒ʂ�ł����A���������G���g���s�[����̖@���̓N���E�W�E�X�̌��������藧�Ƃ���
�ΐ��������Ƃ��ؖ����ꂽ�킯�ł�����A���`�����A�����ɂȂ��Ă��܂���B�������A���̂��Ƃ́A���Ԃ��u�ቷ�����獂�����ɔM�͎��R�ɗ���Ȃ��v�̔�����
��
���o���A�G���g���s�[����̖@����ے�ł���Ƃ������Ƃł�����܂��B�ƂȂ�A�������ۂɂ́A�N���E�W�E�X�̌�����ł��ӂ����m�̃��J�j�Y�������݂���Ƃ�
�����ƂȂ̂ł��傤���B
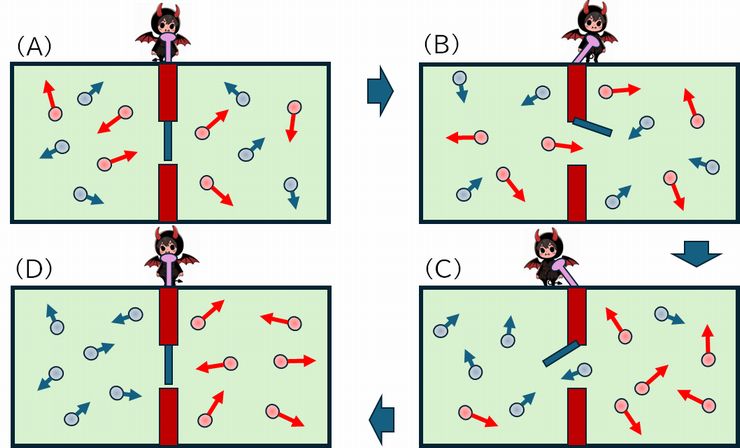
�@�}�b�N�X�E�F���̈����iMaxwell's demon�j�Ƃ́A1867�N����A�X�R�b�g�����h�̕����w�҃W�F�[���Y�E�N���[�N�E�}�b�N�X�E�F���������v�l�����ŁA�����őz�肳���悤�ȉ��炩�̃��J�j�Y������ ������A�M�͊w���@���ŋւ���ꂽ�G���g���s�[�̌������\�ł��邱�Ƃ����N�������̂ł��B�������̎v�l������ے�ł��Ȃ��Ƃ�����A�M�͊w�̍����� �h�邪�����˂Ȃ��킯�ł����A���̓�₪�ꉞ�̌����������͈̂ӊO�ƐV�����A1980�N��ɓ����Ă̂��Ƃł����B
�@�}�b�N�X�E�F�����l�������z�I�Ȏ������e�Ƃ͈ȉ��̂悤�Ȃ��̂ł����B
�@�}9.1�����Ȃ���������Ă����܂��傤�B

�@���܁A�Q�̕�������Ȃ�e�킪�ψ�ȉ��x�̋C�̂Ŗ�������Ă���Ƃ��܂��iA�j�B��3��̍u�`�ł��b�������悤�ɁA���x�Ƃ͋C�̂� ���q�̉^���G�l���M�[�̕��ϒl�ł��̂ŁA�����ŋψ�ȉ��x�Ƃ����Ă����ׂĂ̕��q�̑��x���ψ�Ƃ����킯�ł͂Ȃ��A�������q���x�����q���A���镪�z�������đ��� ���Ă��܂��B�������A�}�ł́A�P���ɑ������q�i�ԁj�ƒx�����q�i�j��2��ނ̕��q����������Ƃ��Ă��܂��B
�@���̗e��̒����ɂ͂Q�̕������u�Ă�ǂ�����܂����A�����ɂ͔��̂� ���������Ȍ����J���Ă��܂��B����A�X�̕��q�̓��������邱�Ƃ̂ł��邠��u���݁v�����āA���̊J ���s�����ƂŁA�C�̕��q�ɒ��ڍ�p���邱�ƂȂ��A�ȉ��ŏq�ׂ�悤�ɁA���̌���ʉ߂���C�̕��q���R���g���[�����邱�Ƃ��ł���Ƃ��܂��B
�@ ���́u���݁v�́A�X�̕��q�̉^�����ώ@���Ă��āA���鑬�����q��������E�ւƌ���ʉ߂���Ɣ��f�����Ƃ� (B)�A���邢�͒x�����q���E���獶�ɒʉ߂���Ɣ��f�����Ƃ� (C)�A���̔����J���܂��B���̑�����J��Ԃ����Ƃɂ��A����ɉE�̕����ɂ͑������q���A�����č��̕����ɂ͒x�����q���W�܂��Ă��܂��B���Ȃ킿�A���q�̉^ ����Ԃ�ω������邱�ƂȂ��A�E�̕����̉��x���グ�A���̕����̉��x�������邱�Ƃ��ł���킯�ł��B����ɂ��A�G���g���s�[�������邱�Ƃ��ł��A���������� ���ĉ��x����������A���̉��x�����g���ĉ��炩�̎d���ݏo�����Ƃ��ł���킯�ł��B
�@�Ƃ���ŁA���̊J�ɂ̓G�l���M�[�͕K�v�Ȃ��Ƃ��܂��B����Ȃ��Ɖ\�Ȃ́A�ƋC�ɂȂ�Ƃ���ł����A�������肵�Ă��A���ǂ́A���̘b�͔ے肳��܂��� �ŁA������ ������Ǝ����Ă����Ă��������B�܂��A�C�̕��q�ɒ��ڎ�������Ă��Ȃ����Ƃ��d�v�ł��B���x�f���A���̊J���߂����Ă��邾���ł��B���ǁA�G�l���M�[ ���g�����ƂȂ��ɁA���́u���݁v�́A�G���g���s�[�̂����Ƃ�������l�ȉ��x�̏�Ԃ���A���G���g���s�[�̒Ⴂ�A���x���̂����Ԃݏo�����Ƃ��ł����̂� ���B����̓G���g���s�[����̖@���ɖ������܂��B���邢�́A�J���m�[�T�C�N �����g�����ؖ��ł̌��ߑ䎌�u�ቷ�����獂�����ɔM�͎��R�ɗ���Ȃ��v���g���Ȃ����ƂɂȂ�킯�ŁA���́u���݁v�̂���V�X�e���ł́A�G���g���s�[����̖@���� �K�p����Ȃ����ƂɂȂ�܂��B
�@���́u���݁v���}�b�N�X�E�F���̈����Ƃ�����̂ł��B�������A������������������Ƃ������Ƃł͂Ȃ��A���̖������s�������Ƃɑ������鉽�炩�̕���
�w�I
�Ȏd�g�݁A���Ȃ킿�A���q��U�蕪���邾���ŁA�d�������邱�ƂȂ��Ɂi�G�l���M�[���g�����ƂȂ��Ɂj���x�������o����d�g�݂����R�E�ɑ��݂���A�G���g���s�[
����̖@����ے�ł���ƌ��������킯�ł��B
�@�}�b�N�X�E�F���̈����͖{���ɃG�l���M�[���g�킸���x���ݏo���Ă���̂ł��傤���H�}�b�N�X�E�F���̈���������Ă��邱�Ƃ͎��̂S�̃X�e�b�v�ɕ����čl �����܂��B
1�D�����́C���ł����C�̗��q���������ǂ������ϑ�����B
2�D�ϑ����ē��������L������B
3�D���𑀍삵�ċC�̕��q��ʉ߂�����B
4�D��ɓ����L�����������Ď��̋C�̗��q�̊ϑ��ɔ�����B
�@�����A���̊J���߂ɃG�l���M�[���K�v�Ȃ��Ƃ��Ă��A�P�̋C�̕��q�̉^�����ϑ����邽�߂ɂ̓G�l���M�[���K�v�ł���A�Ƃ��ă}�b�N�X�E�F���̈����͔ے� ����܂� ���B���������̌�A�P�`�R�ɂ��ẮA�G�l���M�[���g�킸�ɍs�����Ƃ͗��_�I�ɂ͉\�ł��邱�Ƃ�������܂����B�������A4�Ԗڂ́A1�`�R�ōs������������Z�b �g���Ď��̊ϑ��ɔ�����H�������̓G�l���M�[���K�v�ł��邱�Ƃ����̌㎦����܂��B�P�`�R�́A�ꔭ�|�Ƃ��Ă͉\�ł����A�P�`�S���J��Ԃ��s���ɂ͊ϑ����ʂ� �� �x���Z�b�g����K�v������A���̂��߂ɂ̓G�l���M�[��K�v�Ƃ���Ƃ����̂ł��B�ڍׂ͏ȗ����܂����A���ǁA�P�`�S���ЂƂ܂Ƃ߂ɂ��ĕ��q�̉^���̊ϑ��ƒ�`�� ��A�}�b�N�X�E�F���̈����́A���̊J���߂ɂ̓G�l���M�[���g��Ȃ��Ƃ��Ă��A���q�̑��x�Ƃ��������J��Ԃ����邽�߂ɂ̓G�l���M�[���g�킴��Ȃ��� �Ƃ������� ���̂ł��B��͂�A�G���g���s�[�������邽�߂ɂ̓G�l���M�[���K�v�ł���Ƃ������Ƃɗ����������킯�ł��B
�@�}�b�N�X�E�F���̈����́A�����A�M�͊w�̑�2�@����j�郁�J�j�Y�������邩�H�Ƃ�������N�������̂ł����A���݂ł́A�G�l���M�[���g���ď�����ɂ� ��C����ɂ���ċC�̕��q�ɒ��ړ��������邱�ƂȂ����̓����𐧌䂵�A�G���g���s�[�������郁�J�j�Y���Ɋւ�����A�Ɨ�������Ă��܂��B
�@�N�[���[��①�ɂ̂悤�ɁA�d�C�̃G�l���M�[���g���A�ቷ�����獂�����ւƔM�𗬂��A�G���g���s�[�������邱�Ƃ��ł��܂��B�������A�d�C�̃G�l���M�[�� �g�� �����ƂŐ�����G���g���s�[�����������A�S�̂Ƃ��ẴG���g���s�[�͑��債�Ă��܂��B�}�b�N�X�E�F���̈������A���������ď��邽�߂ɃG�l���M�[���g ���A����Ő������G���g���s�[����������A�S�̂Ƃ��Ă̓G���g���s�[�͂�͂葝�債�Ă���Ƃ������ƂɂȂ�܂��B�������A�ǂꂾ�����傷�邩�Ƃ����_�܂ōl ����ƁA���邽�߂̃G�l���M�[�͔�r�I�������čςނ��Ƃ������A�G���g���s�[�̑����Ⴍ�}���邱�Ƃ��ł��܂��B�G���g���s�[�����Ⴍ�}���Ȃ���A�� ���I�ɃG���g���s�[�̒Ⴂ��Ԃ����o�����@�̈�Ƃ��ď���ɗ����낤���Ƃ��A���̂��Ƃ͎������Ă��܂��B�����Ă���ɁA�G���g���s�[�� �u���v�Ɩ��� �ɊW���������ʂł��邱�Ƃ��������Ă���̂ł��B
�i���j�X�[�p�[�R���s���[�^�́A�c��̏��������ɏ������邽�ߐi���������Ă��܂��B�������A����
�Ŗ��ƂȂ�́A����d�͂̑����Ɣr�M�̑����ł��B�X�[�p�[�R���s���[�^�̐i���ɂ́A�d�͐ݔ��Ɨ�p�ݔ��̑啝�ȑ������K�v�ƂȂ�܂��B�܂��A�g�߂ȗ�ł��A
�p�\�R�������炭�g���Ƃ��Ȃ�M���Ȃ邱�Ƃ͂悭�o�����邱�Ƃł��B���邽�߂̃G�l���M�[�͔�r�I�������čςނƂ͂����A���x�ȏ��������ɏ������A
���ʂ悤�Ǝv���Ύv���قǑ����̃G�l���M�[��K�v�Ƃ��A�����̃G���g���s�[��r�o���邱�ƂɂȂ�܂��B
�@�}�b�N�X�E�F���̈����ɂ��āA2010�N�A���{�ʼn���I�Ȏ������s���܂����B�Ő�[�̘b�ł��̂őS�e�𗝉����邱�Ƃ͓���̂ł����A���̕��͋C��
���ł������Ă������������Ǝv���A�����̐V���L�������̂܂܈ȉ��Ɉ��p���܂��i�}�C�i�r�j���[�X�@2010/11/19�j�B
�@������w�Ɠ�����w�̌����`�[���́A�����H�Z�p�ƃT�u�~�N�����X�P�[���̃��A���^
�C������V�X�e����g�ݍ��킹�邱�ƂŁA�u�}�b�N�X�E�F���̈����v�ƌĂ�
��T�O�������Ŏ������A�����G�l���M�[�ɕϊ����邱�Ƃɐ����B����}��ċ쓮����V�K�i�m�f�o�C�X�̎����̉\�����������B
�@"�}�b�N�X�E�F���̈���"
�́A19���I�̕����w�҃W�F�[���Y�E�}�b�N�X�E�F����1867�N�ɍl�����n����̐������ŁA���q�̓������������邱�Ƃ��ł��A�Ⴆ��
���x���̂Ȃ��Ƃ��납��G�l���M�[���g�킸���x�������o���d���������邱�Ƃ��ł���Ƃ���A�M�͊w�ɍ��{�I�ȋ^��𓊂��������B���ꂩ���150�N���o�āA
���̋^��͉������ꂽ���A���ƃG�l���M�[�̊W���l���鑽���̌����ɂȂ������B
�@�Ԃ̃G���W���͔R����R�₵�ĉ��x�������A����ɂ��s�X�g�������ē��삷��B�������A���x�����Ȃ���s�X�g���͓������A�G�l���M�[�����o������ �͂ł��Ȃ��B����͔M�͊w��2�@�� (�G���g���s�[���呥) �Ƃ��Ēm���A�Ȋw�ɂ�����ł���{�I�Ȗ@����1�ƂȂ��Ă���B�������A1867�N�A�����w�҂� �W�F�[���Y�E�N���[�N�E�}�b�N�X�E�F���́A���z�I�Ȉ��� ("�}�b�N�X�E�F���̈���") ���l���A���̖@���ɋ^���˂��t�����B���̈��� �́A���q�̓������ώ@���A����ɉ����ăV�X�e���𐧌䂷��B����ƁA���x�����Ȃ��Ƃ��납��G�l���M�[�����o���A�M�͊w��2�@����j�邱�Ƃ��ł���悤�Ɍ����Ă��܂��B ����́A�Ȋw�j��̏d��ȃp���h�b�N�X�Ƃ��Ēm���A�M�͊w��2�@���ɍ��{�I�ȋ^���˂��t���邱�ƂƂȂ����B���ꂩ���150�N���o���A�}�b�N�X�E�F���̈� ���̓p���h�b �N�X�ł͂Ȃ��A������������������̂ɕK�v�ȃG�l���M�[���܂߂�A�M�͊w��2�@�����j��Ȃ����Ƃ����������B�������A���̗����̉ߒ��ŁA����œ������� ��Â��Đ�����s������ (�t�B�[�h�o�b�N����) �ɂ������G�l���M�[�ɕϊ��ł���Ƃ����T�O�����܂ꂽ�B�����A�Ȋw�I�ɏd�v�Ȃ��̂ł���ɂ��ւ�炸�A���� ���-�G�l���M�[�ϊ��͖����Ɏ����ł��Ă��Ȃ��̂�����ł������B
�@�����̊T�O�͂܂��A�点��K�i�̏�ŔM�h�炬�ɂ���ă����_���ɉ^���i�u���E���^���j���闱�q���l����B���q�͏�ɃX�e�b�v�����艺�ɃX�e�b�v�����肷�� ���A ���z������̂ŁA���ϓI�ɂ͊K�i������B�������A�Ⴆ�A���q�̈ʒu�𑪒肵�A���q����ɃX�e�b�v�����痱�q�̌��ɕǂ�u���B�ĂсA���q����ɃX�e�b�v���� �痱�q�̌��ɕǂ�u���B������J��Ԃ��ƁA���q�ɊK�i��o�点�邱�Ƃ��ł���Ɗ��҂ł���B�ǂ�u���̂ɗ��z�I�ɂ̓G�l���M�[���K�v�Ȃ����Ƃ��m���Ă� ��B���������āA�O����G�l���M�[�����������ɁA���q�ɊK�i��o�点�邱�Ƃ��ł���B����́A�t�B�[�h�o�b�N����ɂ������G�l���M�[�ɕϊ����邱�ƂŁA�� �q���쓮�ł����Ɖ��߂ł���B
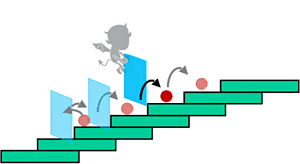
�}9.2�@���G�l���M�[�ݏo�������̌���
�@�}�b�N�X�E�F���̈����́u�I�ʁv���邢�́u�I���v�Ƃ����s�ׂɂ���ăG���g���s�[�����������A�Ђ��Ă͒����ݏo���Ă���ƌ����܂��B�����A�}�b�N�X�E�F
���́A���́u�I���v�Ƃ����s�ׂ̏d�v���ɋC�Â��܂���ł������A���̌�̌����҂����ɂ���Ă��̏d�v�����C�Â��ꂽ�Ƃ����킯�ł��B���́A���́u�I���v�Ƃ���
�s
�ׂ́A����ꂪ���i�u���v�Ƃ��ł�����̂Ɩ��ڂɊW���Ă��܂��B�����ŁA�}�b�N�X�E�F���̈����̘b�͂����܂łƂ��A������蓹�����āA�㔼�͏�_�Ƃ����H�w��
�����
��������̃G���g���s�[�Ƃ������b�������܂��B����ɂ��A�G���g���s�[���u���v�Ɩ��ڂɊ֘A�����ʂł��邱�ƁA�u�I���v�Ƃ����s�ׂ������Ɩ��ڂɊ�
�A���Ă��邱�ƂȂǂ��킩���Ă��������邩�Ǝv���܂��B
(1) �����Ȃ�ł����A��_�ł́A���������炷���ۂ̐��N�m���i�N����m���j\(p\) ���g���āA���̎��ۂ��N�������ƒm�炳�ꂽ�Ƃ�������ʂ� \(I(p) = - \log_{2} p \) (�P�ʁ@bit�G�r�b�g)�@�ƒ�`���܂��B���̎����Ӗ�����Ƃ�����A��̓I�ȗ�̒��ŗ������Ă����܂��傤�B
�k��1�l�R�C���𓊂���܂ł͕\���o�邩�A�����o�邩�킩��܂���B�����ɕ\���o���Ƃ��������Ƃ����Ƃ��A�\���o��m�����@\(p =
\frac{1}{2} \) �Ȃ̂ŁA\( I(p) = - \log_{2} \frac{1}{2} = 1 \) �r�b�g�̏����Ƃ����܂��B
�k��2�l���l�ɁA�T�C�R���͓�����܂ł͉��̖ڂ��o�邩�킩��܂���B�����ɃT�C�R���łT�̖ڂ��o���Ƃ��������Ƃ���ƁA�T�̖ڂ��o��m����
\(p = \frac{1}{6} \)�@�Ȃ̂ŁA\( I(p) = - \log_{2} \frac{1}{6} = 2.59 \)
�r�b�g�̏������ƂɂȂ�܂��B�R�C���̗��\�̏������A�T�C�R���̖ڂ̏��̕����A���ʂ�2.59�{���傫���Ƃ������ƂɂȂ�܂��B
�k��3�l�����T�C�R���̏ꍇ�ł��A�����̖ڂ���̖ڂ������ɋ���������ꍇ�A�T�̖ڂ��o���Ƃ����̂͊�̖ڂ��o���Ƃ����Ӗ���������܂���̂ŁA��̖�
���o��m�����@\(p = \frac{1}{2} \)�@�Ȃ̂ŁA\( I(p) = - \log_{2} \frac{1}{2} = 1
\) �r�b�g�̏����Ƃ������ƂɂȂ�܂��B
�k��4�l�K���N����o�������N�������Ƃ����ꍇ�� \( p=1 \) �Ȃ̂ŁA\( I(p) = - \log_{2}1 = 0
\) �r�b�g�ŁA���ʂ͂Ȃ��Ƃ������Ƃł��B
�@���Ȃ킿�@\( I(p) \geq 0 \)�@�Œ�`����Ă��邱�ƂɂȂ�܂��B
�@���ǁA���ʂƂ́A���鎖�ۂ��N����m���ɂ������ʂŁA�ǂ̎��ۂ��N���邾�낤���Ɛ��肵�Ă���Ƃ��̂킩��Ȃ��̓x�����ɊW�����ʂƂ����܂��B�������A�Ȃ��m����
�̂��� �ł͂Ȃ��A���̑ΐ��ŕ\�������̂ł��傤���B
(2) �����łQ�̓Ɨ��ȏ��A�AB������ꍇ���l���܂��BA�AB�ɂ͂��ꂼ����������炷���ۂ���������A���̒��̂��鎖�ۂ��N����m�������ꂼ�� \(p_{A}\)�A\(p_{B}\) �Ƃ��܂��B����ƁA����炪�����ɋN����m���� \(p_{A} \times p_{B} \) �ƂȂ�܂��B���̂Ƃ��A����炪�����ɋN�������ƒm�����Ƃ��̏��ʂ͎����ŗ^�����܂��B
\( I(p_{A}, p_{B})= -
\log_{2}p_{A}�~p_{B} = - \log_{2} \, p_{A} - \log_{2} \, p_{B}=
I(p_{A})+I(p_{B}) \)
�@���������āA�����ɋN���������Ƃɂ���Ă����炳�ꂽ���� \(I(p_{A}, p_{B} ) \) �́A�ʂɋN�������Ƃ��ɂ��ꂼ�ꂩ�瓾������� \( I(p_{A}) \) �� \(I(p_{B}) \) �̘a�ŕ\����܂��B
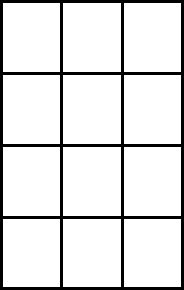 �k�� 5�l4�s3��ŗ��Ԃ��ĕ��ׂ��g�����v������Ƃ��܂��B�ǂ�����♡A������܂��B
�k�� 5�l4�s3��ŗ��Ԃ��ĕ��ׂ��g�����v������Ƃ��܂��B�ǂ�����♡A������܂��B
�@ �E�[�̗�ɂ���ƒm�炳�ꂽ�Ƃ��̏��ʂ�
�@�ǂ̗�ɂ��邩�͊m�� \( p = \frac{1}{3} \)�@�ł��̂ŁA
\( I(p) = - \log_{2} \frac{1}{3} = 1.58 \) �r�b�g�@�ƂȂ�
�A �ォ��2�s�ڂɂ���ƒm�炳�ꂽ�Ƃ��̏��ʂ�
�@�ǂ̍s�ɂ��邩�͊m�� \(p = \frac{1}{4} \)�@�ł��̂ŁA�@
\( I(p) = - \log_{2} \frac{1}{4} = 2 \) �r�b�g�@�@�ƂȂ�܂��B
�B ����A�E�[�̗�̏ォ��2�s�ڂɂ���ƒm�炳�ꂽ�Ƃ��̏��ʂ�
�@12���̃J�[�h�̂����̂ǂ̏ꏊ�̃J�[�h�ł��邩�͊m�� \(p = \frac{1}{12} \) �ł��̂ŁA
\( I(p) = - \log_{2} \frac{1}{12} = 3.58 \) �r�b�g
�ƂȂ�܂��B
�@�Ƃ���ŁA�E�[�̗�ɂ��邱�Ƃ��܂��m���āi���̂Ƃ� \(1.58\) �r�b�g�̏��܂��j�A����ɏォ��2�s�ڂł��邱�Ƃ�m�����i���̂Ƃ������2�r�b�g�̏��܂��j�ƍl����A\( 1.58 + 2 = 3.58 \) �r�b�g�̏������ƂƂȂ�A�B�̍s�Ɨ�̗����ɂ��ē����ɒm�����Ƃ��̏��ʂƈ�v���܂��B���ŕ\���A
\( I(p) = - \log_{2}
\frac{1}{12} = - \log_{2} \frac{1}{3} \times \frac{1}{4} = -
\log_{2} \frac{1}{3} - \log_{2} \frac{1}{4} = 3.58 \) �r�b�g
�ƂȂ�܂��B��������̉��@���ƌĂт܂��B�ΐ��Ƃ������́A�ς�a�ɕϊ�����@�\������܂��̂ŁA���N�m���ƌ��ѕt���A���̉��@����F�߂�ƁA��
���������ʂ̒�`�������Ƃ������I�Ƃ�����̂ł��B
(3) �ꍇ�̐����邢�͑I�����̐��Ə���
�@�������琶�N����鎖�ۂ̏ꍇ�̐��� \(W\) �ŁA����������炪���ׂē��m���ŋN����Ƃ��A�X�̎��ۂ̐��N�m���� \(p =
\frac{1}{W} \) �ƂȂ�܂��B���������āA\(W\) �̉\�Ȏ��ۂ̂������鎖�ۂ��N�������ƒm�炳�ꂽ�Ƃ���������̗ʂ́A\( -
\log_{2} \frac{1}{W} = \log_{2} W \) �ƂȂ�܂��B���Ȃ킿�A���ׂĂ̎���
�����m���Ő��N����ꍇ�A���ʂ́A���N����鎖�ۂ̏ꍇ�̐��i���邢�͑I�����̐��ƌ���������Ƃ킩��₷���ꍇ������܂��j�̑ΐ��Ƃ��Ē�`����܂��B
�k��6�l����l�� 1 ���� 64�i��26�j�܂ł̐����������߂Ă��炢�A������l�����̐��� yes �܂��� no
�œ������鎿������ē��Ă邱�Ƃ��l���܂��Byes �܂��� no �̓����œ�������ʂ́A�I�����i���邢�͏ꍇ�̐��j���Q�Ȃ̂ŁA\(
\log_{2} 2 = 1 \) �r�b�g�ł��B����A���͑I�����̐���64�ŁA���̂����̈����肵���Ƃ��̏��ʂ́A\( \log_{2} 64
= 6 \) �r�b�g�ł��B���������āA�ő�ł�6��� yes �܂��� no
�œ������鎿������邱�ƂŁA���̐����������Ă邱�Ƃ��ł���i6��̎����6�r�b�g�̏��邱�Ƃ��ł��邩��j�͂��ł��B
�@��̗���l���܂��傤�B���߂�������18�Ƃ��܂��傤�B����Ɠ����������܂��B
�@�@�@32���傫�����ł����H�|No�@�s1�`32�̐��ł��t�@�@�@�s�c�t�͓���ꂽ���
�@�@�A16���傫���� �ł����H�|Yes �s17�`32�̐��ł��t
�@�@�B24���傫�����ł����H�|No�@�s17�`24�̐��ł��t
�@�@�C20���傫�����ł����H�|No�@�s17�`20�̐��ł��t
�@�@�D18���傫�����ł����H�|No�@�s17�`18�̐��ł��t
�@�@�E18�ł����H�|Yes�@
�ƂȂ�܂��B1�`64
���ɂ��Ă��̂ǂ���̃O���[�v����q�ˁA������ƍ��x�́A�܂܂�Ă����O���[�v���ɂ��ē������Ƃ��J��Ԃ��킯�ł��B���̓s�x�A�I�����̐��͔����ƂȂ�A����
log2(�I�����̐�) ��1�r�b�g�������Ă����܂��B
(4) ���̃G���g���s�[�i��������ʂ̊��Ғl�j
�������� \(W\) ��ނ̎��ۂ����N����\��������A�����̐��N�m�������ꂼ�� \(p_{i}\)
(\(i=1,2,...,W\)) �ŗ^������Ƃ��A���̏�̂����ς̏��ʁA���邢�͓�������ʂ̊��Ғl��
�@�@�@\[ H = \sum_{i=1}^{W} - p_{i} \log_{2} p_{i} �@�@�������@
\sum_{i=1}^{W} p_{i} = 1 \]�@ �@
�ƂȂ�܂��B��������̃G���g���s�[�ƌĂт܂��B
�@���ɁA���ׂĂ̎��ۂ����m���Ő��N����ꍇ�A���Ȃ킿 \( p_{1} = p_{2} = \cdots = p_{W} =
\frac{1}{W} \) �@�̂Ƃ��A���̃G���g���s�[�͍ő�ƂȂ�A\( H = \log_{2} W \) �ƂȂ�܂��B
�@���̃G���g���s�[�́A��������ʂ̕��ϒl�i���Ғl�j���Ӗ����Ă��܂��B��������� \( - \log_{2} p_{i} \)
�Ƃ��ꂪ�N����m�� \( p_{i} \)
���|�������̂����ׂĂ̎��ۂɂ��đ������Ƃœ����܂��B�܂��A���ׂĂ̎��ۂ����m���Ő��N����ꍇ�A���ʂ́A���N����鎖�ۂ̏ꍇ�̐��̑ΐ��ŗ^�����܂��B
�i���j����ʂƂ��ꂪ�N����m���������āA���ׂĂ̏ꍇ�ɂ��ĉ�����ƕ��ϒl�ƂȂ�Ƃ����̂�������ɂ����Ƃ������̂��߂ɁA�ȒP�ȗ�������Ă����܂��B
�@���܁A�̏d��50kg�̐l��3�l�A60kg��5�l�A70kg��2�l���܂��B����10�l�̕��ϑ̏d
���l���܂��B
�@�@\( ( 50 \times 3 + 60 \times 5 + 70 \times 2 ) ��10�@= 50 \times
\frac{3}{10} + 60 \times \frac{5}{10} + 70 \times \frac{2}{10} \)
�ƂȂ�܂��B(�̏d)�~(���̑̏d�ł���m��)�@�����ׂĂ̑̏d�ɂ��Ęa���Ƃ�Ƃ����`�ɂȂ��Ă��܂��B
�k��7�l���̃G���g���s�[���A���ۂ��Q�̏ꍇ�A�R�̏ꍇ�ɂ��Čv�Z���Ă݂܂��傤�B���N�m�����قȂ�ꍇ�ɂ��Čv�Z���Ă݂�ƈȉ��̂悤�ɂȂ��
���B
�@�@�@�Q�̎��ۂ̐��N�m�� �@�@�@�@�R�̎��ۂ̐��N�m��
�@�@�@ A�@ B�@ ���G���g���s�[ A�@ B �@
C�@���G���g���s�[
�@�@�@1/2 1/2 1 �r�b�g
�@ �@�@�@1/3 1/3 1/3 1.58 �r�b�g
1/5
4/5 0.72
�@�@ �@�@�@ 2/5 2/5 1/5 1.52
2/5
3/5 0.97
�@�@ �@�@ 3/5 1/5
1/5 1.37
�@���ׂĂ̎��ۂ����m���ŋN����Ƃ��A���̃G���g���s�[�͍ő�ƂȂ邱�Ƃ��ؖ�����Ă��܂��B���N�m���ɕ肪����Ə��̃G���g
���s�[�͏������Ȃ�܂��B
�k��8�l�����ړ����`�� \(N\)
�̋ʂ�����A�P�������A���ׂē����d���ł���Ƃ��܂��i��O�̋ʂ͑��̋ʂ��y���Ƃ��܂��j�B���������V���Ōv�ʂ���Όy���ʂ��m���Ɍ�������ł��傤���B
�@�܂��A�����`�̂��� (1�ł��A�����ł��悢�B�����������̏ꍇ�͗��V���M�ɓ����������̂Ƃ��܂�) ��V���Ōv�����Ƃ���������ʂ��l���Ă݂܂��傤�B�V���ŏd�����r���鎎�s�ɂ���āA�u�E�̎M�v�u���̎M�v�u�V���O�v��3�̃O���[�v�̂ǂ��Ɍy���ʂ����邩��m�� ���Ƃ��ł��܂��B���������đI������3�ł�����A1��̎��s�œ�������ʂ́@\( - \log_{2} \frac{1}{3} = \log_{2} 3 ��1.6 \) �ޯĂƂȂ�܂��B������ \(k\) �s����A\(k \log_{2} 3 = 1.6 k \) �ޯĂ̏��邱�Ƃ��ł��܂��B�i�R�̃O���[�v�Ɋ܂܂��ʂ̐����قȂ邱�Ƃ��l������ƁA��������ʂ͑����قȂ��Ă��܂����A�����ł͂����܂ōl���Ȃ����� �ɂ��܂��j
�@���Ƃ��A�����`�̂V�̋ʂ�����P�����y���ʂ��������Ă���Ƃ��A���̌y���ʂ����R�݂���m���� \( \frac{1}{7} \) �ł��̂ŁA�����m�����Ƃ��̏��ʂ� \( - \log_{2} \frac{1}{7} = \log_{2} 7 = 2.8 \) �ޯĂƂȂ�܂��B����A\( k = 2\) ��̎��s�� \(1.6 \times 2 = 3.2 \) �ޯĂ̏������܂��̂ŁA2��̎��s�Ōy���ʂ������邱�Ƃ��ł���͂��ł��B
�@���ہA7���i3�A3�A1�j�ɂ킯�A3���m��V���ɂ����܂��B�����ލ����A�c��1���y���Ƃ킩��܂��B�ލ���Ȃ���A�y������3�̂�����
��2
��I�сA1���V���M�ɏ悹�܂��B�ލ����Ύc��1���y���ʂł����A�ލ���Ȃ������Ōy�������T���Ă���ʂƂ������ƂɂȂ�܂��B���ǁA2��̎��s��
�y���ʂ���肷�邱�Ƃ��\�ƂȂ�܂��B
�k��9�l �����̗̂e�킪 (A) ���邢�� (B) �Ŏ������悤�ɐςݏグ���Ă��܂��B\(N\)
�̗��q������痧���̗̂e��̂ǂꂩ�Ƀo���o���ɂȂ��Ă͂����Ă��܂��B��̗e��ɕ��������Ă��Ă������ł����A�܂�����
�����Ă��Ȃ��e�킪�����Ă��\���܂���B���ׂĂ̗��q�ɂ��āA�ǂ̗e��ɂ��邩�m�����Ƃ���������ʂ̊��Ғl�A���Ȃ킿���̃G���g���s�[��
(A)�A(B) ���ꂼ��ǂ̂��炢�ł��傤���B
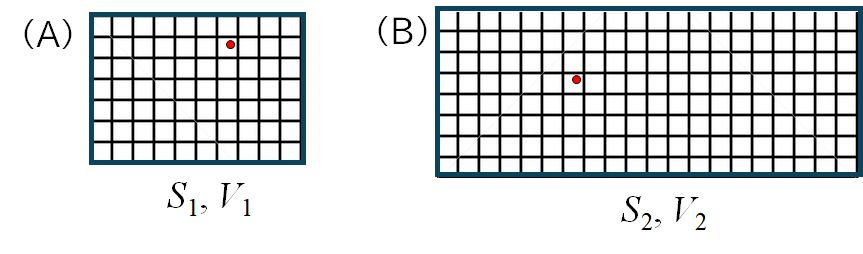
�}9.4�@�傫�Ȓ����̂̋�Ԃ������ȗ����̂ŋ��A\(N\) �̗��q���ǂ��ɂ��邩���l���܂�
�@��̗��q�ɒ��ڂ��܂��B�ǂ̗����̂ɂ��邩�A���̏ꍇ�̐��� (A) \(V_{1} = 70 \)�A�@(B) \( V_{2} =
160 \) �ł�����A���̃G���g���s�[�͂��ꂼ�� \( H_{1} = \log_{2} V_{1} = \log_{2} 70 \)�A \(
H_{2} = \log_{2} V_{2} = \log_{2} 160
\)�@�ƂȂ�܂��BN�̗��q�͂��ꂼ��Ɨ��ł��̂ŁA���̉��@���ɂ��A�S���̃G���g���s�[�� \( H_{1} = N \log_{2}
V_{1} = N \log_{2} 70 \)�A \( H_{2} = N \log_{2} V_{2} = N \log_{2} 160 \)
�ƂȂ�܂��B���������āA���҂̏��̃G���g���s�[�̍���
\( H_{2} - H_{1} = N \log_{2} V_{2} - N \log_{2} V_{1} = N \log_{2}
\frac{V_{2}}{V_{1}} = N \log_{2} \frac{160}{70} = N \log_{2} \frac{16}{7}
\)�@�ƂȂ�܂��B
�@�Ƃ���ŁA��10��u�`�����́@10.2 �G���g���s�[�̌v�Z�@�̗� (1)�ŁA�̐ς� \( V_{1} \) �� \( V_{2} \)
�̃G���g���s�[�������߂܂����B���ꂼ��̃G���g���s�[�̒l�� \( S_{1} \)�A\( S_{2} \) �Ƃ���ƁA���̍���
�@\( S_{2} - S_{1} = nR \log \frac{V_{2}}{V_{1}} \)
�ł����B�����ŁA������ \(n\) �͑S���q�̐��� \(N\)�A�A�{�K�h������ \(N_{AV}\) �Ƃ���� \( n =
\frac{N}{N_{AV}} \) �ƕ\����܂��̂�
�@\( S_{2} - S_{1} = \frac{R}{N_{AV}} N \log \frac{V_{2}}{V_{1}} \)
�ƂȂ�܂��B\( H_{2} - H_{1} \) �� \(S_{2} - S_{1} \) ���r����ƁA���҂́A�W�� \(
\frac{R}{N_{AV}} \)
�Ƒΐ��̒ꂪ�Ⴄ�ɂ����܂���B�G���g���s�[�Ƃ����ʂ��A���Ɩ��ڂɊւ���Ă������Ƃ��A�������Ď����ꂽ�킯�ł��B
�@�����w�ɂ�����G���g���s�[�͂����܂ł����q�̔M�^���Ɋ�b�����������̂ł��B���������āA�����̎U�炩��͕����w�I�ȈӖ��ł̃G���g���s�[�Ƃ͈قȂ�A��
�_�I�ȃG���g���s�[�ł���ƑO�b�����܂����B�������A��ň��p�����V���L���̂悤�ɁA�~�N���̐��E�ɂ����ƁA�����w�I�G���g���s�[�Ə�_�I�ȃG��
�g
���s�[�͑��݂Ɋ֘A�������A���q�̔M�^���Ɋւ�������ϑ����邱�ƂŁA�����G�l���M�[�ɕς��邱�Ƃ��\�ƂȂ�܂��B�܂��A�O��̖`���ŃG���g���s�[�Ɋ�
���Đ���ɔ����I��Ԑ��Ɍ��y���Ă������R���A���ʂ��ꍇ�̐��̑ΐ��ŕ\������邱�Ƃ���[���ł����̂ł͂Ȃ��ł��傤���B
�@�Ƃ���ŁA�`���Ɍf�����������ۂƃG���g���s�[����̖@���Ƃ̊W�͌��ǂǂ��Ȃ����̂ł��傤���B�}�b�N�X�E�F���̈����Ɉ�r�̖]�݂�������̂ł����A�c�O �Ȃ���������܂���ł����B�������ۂƃG���g���s�[����̖@���Ƃ̊W�ɂ��Ă͎���ւƐ摗��ł��B����͂����܂łƂ��܂��B

�u
���E���E���`�F�b�g�i�O�������N Wikipedia�j