今回と次回は、おそらく今まであまり出会ったことのないような議論が続きます。この話題は省略して結果だけを示してもよかったのですが、ここで行われる論理展開 は自然科学独特だと思いますので、そうしたことに触れていただくことも意味があるだろうと思い、敢えて講義内容に加えました。論理の展開がよく理解できないと 抵抗 感を抱くとしたら、一つには非常に一般化した議論であること、抽象化した議論であることが原因かもしれません。しかし、だからこそ普遍的な証明になっているという 側面がありますので、何とか楽しんでいただければ幸いです。
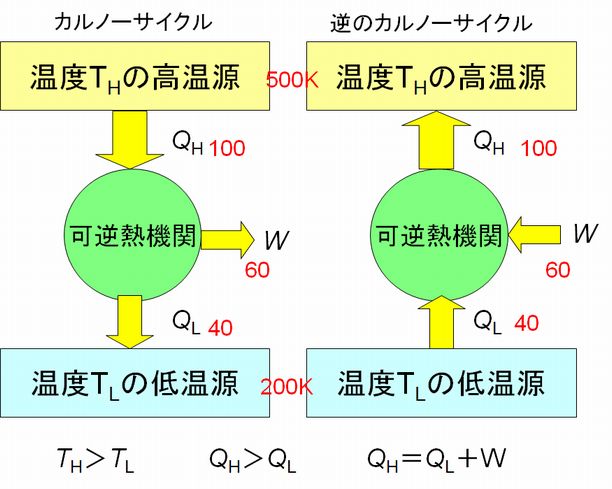
第5回の講義でカルノーサイクルの説明をしました。そこではカルノーサイクルが仕事を生み出す詳細な説明をしましたが、これからは図6.1に示すような簡略化した図 を用いて、その特性を見ていこうと思います。
可逆熱機関と書いた円はカルノーサイクルを表しています。実は、単に簡略化したというだけでなく、可逆な熱機関ならばカルノーサイクルでなくてもこれからの話は 成立するという意味で、より一般化した表現でもあるのです。可逆熱機関とは、図6.1の左のように、高温源から熱 \(Q_{H}\) を奪い、低温源に熱 \(Q_{L}\) を捨てることで外に向かって仕事 \(W\) を生み出すことも、図6.1右のように、その逆回転によって、外から仕事 \(W\) をその機関に対して行うことによって、低温源から熱 \(Q_{L}\) を奪い、高温源に熱 \(Q_{H}\) を捨て ることもできる熱機関で、大切なことは、どちらの \(Q_{H}\)、\(Q_{L}\)、\(W\) も同じ値であるということです。これが異なる場合には、不可逆な熱機関ということになります。

可逆熱機関では、高温源と低温源の温度 \(T_{H}\)、\(T_{L}\) と、入力と出力の熱 \(Q_{H}\)、\(Q_{L}\) との間に次の関係が成り立つことを導くことができます。
\[ \frac{T_L}{T_H}=\frac{Q_L}{Q_H} あるいは \frac{Q_{L}}{T_{L}}= \frac{Q_{H}}{T_{H}} \tag{1} \]
この式の導出は、この資料の最後の「可逆熱機関における熱源の温度…」にありますので、興味のある人は参照してください。
ここで、熱機関の効率 \( \eta \) を定義しておきます。熱機関の効率とは、高温源から取り出した熱 \(Q_{H}\) のうちどれくらいを仕事 \(W\) に変換することができるのか、その割合のことをいい、次式で与えられます。
\[ \eta= \frac{W}{Q_{H}} = \frac{Q_{H}-Q_{L}}{Q_{H}}=1-\frac{Q_{L}}{Q_{H}} \tag{2} \]
式の変形にはエネルギー保存の法則 \(Q_{H} = Q_{L} + W \) を使いました。高温源から取り出した熱 \(Q_{H} \) をすべて仕事に変換することができれば \(Q_{H} =W \)、\(Q_{L} = 0 \) ですので、効率 \( \eta = 1 \) となります。まったく仕事に変換できなければ \(W = 0 \) ですので、\( \eta = 0 \) です。 可逆熱機関では(1)式より
\[ \eta=1-\frac{Q_{L}}{Q_{H}}=1-\frac{T_{L}}{T_{H}} \tag{3} \]
となります。したがって、可逆熱機関では、高温源と低温源の温度が決まると、その作動原理が何であろうと、効率は一義的に決まってしまうことになります。
準備が整いましたので、いよいよ証明にはいりますが、何を証明したいかをまず説明しておきましょう。
熱機関には、これまで取り上げたニューコメンやワットの蒸気機関、カルノーサイクルだけでなく、自動車のガソリン・エンジンなど身近なものでもさまざまな ものが あります。また、これからも新たな熱機関が次々と開発されてくるでしょう。大天才が現れて、現時点ではまったく想像も出来ないような新規な方法による熱機関も 登場 するかもしれません。しかし、それでも、カルノーサイクル(広く可逆熱機関)よりも効率のよい熱機関は絶対にできないことをこれから証明します。でも、“想像も出来 ないような新規な方法による熱機関” も含めて、そんな証明ができるのでしょうか。それでも証明できるのです。それが今回、そして次回の講義の醍醐味であり、皆 さんに見ていただきたいポイントです。
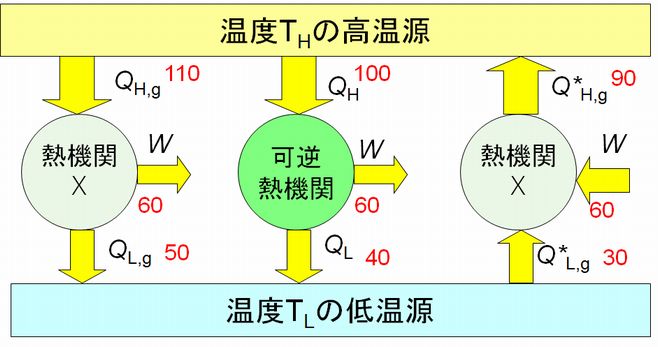
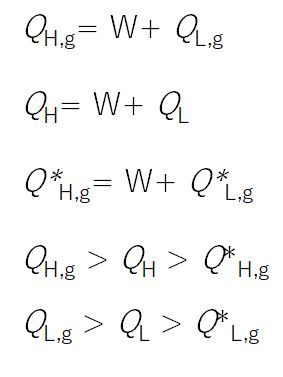
さらに、逆のカルノーサイクルについても、この効率を超える熱機関は存在し得ないことを証明します。これにより、熱機関は、可逆であれば、そ の効率はカルノーサイク ルに等しく、不可逆ならば、その効率はカルノーサイクルの効率も逆のカルノーサイクルの効率も超えることができないことが証明されます。ただし、逆のカル ノーサ イクルについての証明は次回お話しします。 証明したいことを図6.2にまとめました。中央が可逆熱機関、左端が一般の熱機関Xで、右端がそれを逆回転したものです。一般の熱機関Xは、可逆機関と等しいか、より 効率が悪いことが証明されます。
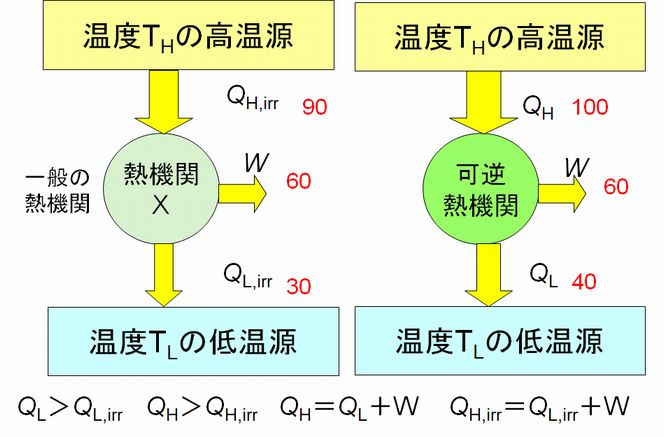
まずは、カルノーサイクル(可逆熱機関)が最も効率のよい熱機関であることを証明します。証明は背理法を使います。すなわち、高温の熱源から \(Q_{H,irr} \) の熱を取得し、低温の熱源に \(Q_{L,irr} \) の熱を捨てることで、外に対して仕事 \(W\) を行うことができる熱機関Xがあり、その効率がカルノーサイクルの効率よりも高いと仮定します(図6.3参照)。 すると何らかの矛盾が生じることを示し、したがって、カルノーサイクルより効率の高い熱機関は存在し得ないという結論に至る、というわけです。
ここで生じる矛盾とは何かというと、クラウジウスの原理に反する事態が生じるのです。 クラウジウスの原理とは、「1つのシステムがサイクルを行なって、低温の物体から熱を受け取り、高温の物体にその熱を与える以外に何の変化も残さないようにするこ とはできない」というものです。
分かりにくい表現かもしれませんが、“何の変化も残さない” を、外部からのエネルギーを使ってエネルギー資源を減少させないと考えれば、エネルギーを使わずして低 温の物体から高温の物体へと熱を流すことはできないということです。もっと具体的に言えば、電気を使わず動くクーラーや冷蔵庫は存在しないということであり、 ぬる ま湯の入ったやかん(高温部)を冷たい水の入った容器(低温部)の中に漬けておいたら、やがて容器の水の温度が更に下がって凍り、熱が流れ込んだやかんの水が沸騰 したということも起こり得ないということです。
この原理は、経験的にそうだろうと誰もが認めますが、実は証明はされていません。エントロピー増大の法則をす でに 知っている人は、エントロピー増大の法則に反するから、と言うかもしれませんが、いまそのエントロピー増大の法則を証明しようとしているので説明になっていませ ん。言い換えれば、クラウジウスの原理が正しければエントロピー増大の法則が証明でき、エントロピー増大の法則が正しければクラウジウスの原理を証明できると いう 論理構造になっていて、結局、証明できていないのです。したがって、これからエントロピー増大の法則を証明しますが、あくまでもクラウジウスの原理が正しければと いう前提付きの証明です。しかし、クラウジウスの原理が間違っているという証明も実例もありませんので、これは正しいとして次のステップに進みます。
図6.4を見てください。
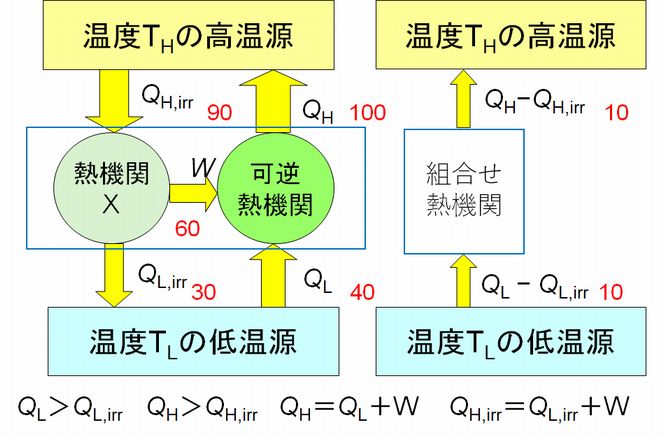
図6.4 熱機関Xと逆のカルノーサイクルとを組み合わせた熱機関
逆のカルノーサイクルを熱機関Xと組み合わせ、熱機関Xが生み出す仕事 \(W\) をすべて逆のカルノーサイクルの運転に使うことにします。逆のカル ノーサイクルと熱機関Xとを組み合わせたものも一つの熱機関とみなすことができます。この組み合わせ熱機関には、外部からエネルギーが供給されていません。に もかかわ らず、低温源から熱 \(Q_{L} − Q_{L,irr} \) を受け取り、高温源へ熱 \(Q_{H} – Q_{H,irr} \) を流しています。これは明らかにクラウジウスの原理に反します。では、なぜこうなったのでしょうか。カルノーサイクルおよび逆のカルノーサイクルは第5回講義 で示したように、理論的に可能な熱機関です。となれば、熱機関Xが問題となります。すなわち、カルノーサイクルより効率がよいと仮定したことがこの矛盾を生ん だ元凶というわけです。結果、カルノーサイクルより効率がよい熱機関の存在が否定されたことになります。
ところで、熱機関Xの内部構造や作動原理については何も言及していません。したがって、どんな素晴らしい天才が登場して、どんな画期的なアイデアで熱機関を作ろう とも、“クラウジウスの原理を認める限り”、このことは成り立つわけです。
ところで、上で証明したことはどのような意味をもつのでしょうか。
そもそもこの議論は、第5回の熱機関の話から始まりました、ニューコメン、ワットの蒸気機関をみると、冷却部分が存在します。燃料を使ってお湯を沸かし、せっか く蒸気を生み出したにもかかわらず、その一部をむざむざと冷却して水に戻してしまう、つまり捨ててしまうのです。そこでカルノーが登場し、この冷却部分をなん とかなくす方法はないか考えていくうちに、カルノーサイクルのアイデアにたどり着いたというわけです。
しかし、カルノーサイクルにおいても、熱を低温源へと捨てています。やはり冷却部分が存在するのです。しかも、上で証明したことは、カルノーサイクルが最 も 効率の 高い熱機関であることでした。結局、熱機関を設計する上で、冷却部分は絶対に必要であることが証明されたのです。これは、言い換えれば、熱をすべて仕事に変換する ことができないことを意味しています。熱を仕事に変換するような熱機関を作っても、その熱の一部を低温源に捨てるという工程を作らないと仕事を生み出すことが できないというのです。
第2回の講義でエネルギー保存の法則の話をしました。エネルギーにはさまざまな形があり、相互に変換が可能であり、変換してもその量は保存される、というもので した。しかし、例外があったのです。熱というエネルギーは、すべて仕事に変換することはできず、一部、どうしても熱という形のエネルギーのままになるのです。 身の 回りをみてください。工場でも廃熱の問題は深刻ですし、料理でガスを使えば熱が出ますし、目の前のパソコンも熱くなります。あなた自身もまわりの空気に放熱してい ます。エネルギーを使うことで必ず熱が発生します。しかしその熱というエネルギーをもう一度利用可能なエネルギーの形に戻そうとしても限界があるということで す。
ここで、応用問題を一つ考えましょう。「図6.5の左のような、一つの熱源だけを使って仕事を生み出す熱機関Aは存在しないことを証明しなさい」。図6.5では低温源に 熱機関Aを接続していますが、高温源に接続しても同じ結論に達します。
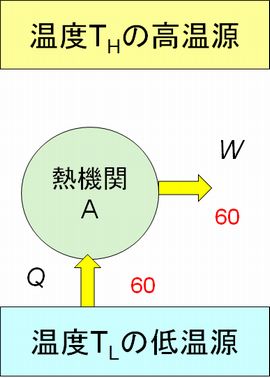
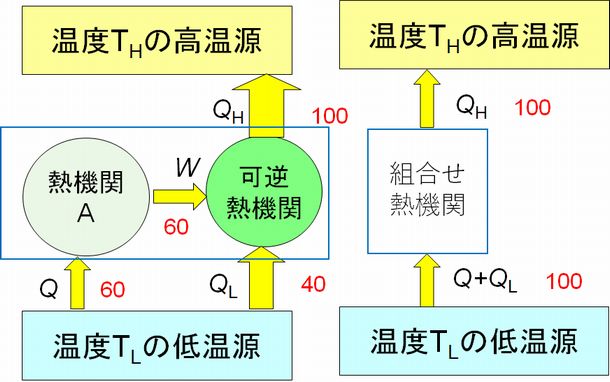
証明方法はこれまでと同様に、逆のカルノーサイクルに熱機関Aを接続します。すると、熱機関Aと逆のカルノーサイクルを組み合わせたものも一つの熱機関と みなせ ます。そしてこの組み合わせ熱機関は外部からのエネルギーを一切供給されることなく、低温源から高温源へと熱を流していますので、クラウジウスの原理に反します。 したがって、熱機関Aの存在が否定されるというわけです。
これをケルビンの原理といいます。物理学の言葉で表現すると、「 ある一定の温度にある熱源から正の熱を取り出し、これに相当する正の仕事を外に向かって行なうようなサイクルは存在しない。」 となります。
ケルビンの原理は次のように表現することもできます。 ある一定の温度にある熱源から正の熱を取り出し、これに相当する正の仕事を外に向かって行なうようなサイクルを第2種の永久機関という。第2種の永久機関は存在し ない。
第2回講義で、エネルギー保存の法則から第1種永久機関は存在しないことを説明しました。エネルギーを使わずしてエネルギーを生み出す機関は存在しないというこ とでした。ここでいう第2種永久機関は、エネルギー保存の法則には抵触しないけれど、一つの熱源から得た熱をすべて仕事に変える機関は存在しないというこ とです。実際、図6.5の熱機関Aは熱を仕事に変換しているだけですから、エネルギー保存の法則には抵触していません。
ケルビンの原理は、言い換えれば、熱を仕事に変換するためには、温度の異なる2つの熱源が必要だということです。このことは、上で述べたカルノーサイクルの効率に 関する式(3) \( \eta=1-\frac{T_{L}}{T_{H}} \) でも確認できます。低温源 \(T_{L} \) と高温源 \(T_{H} \) が等しいとき、すなわち \( \frac{T_{L} }{ T_{H}} = 1 \) のとき、効率は \( \eta = 0 \) となり、仕事が発生しないことを示しています。そして、いかなる熱機関もカルノーサイクルの効率を超えることができないわけですから、いかなる熱機関も低温源と高温源の温 度差がない状況、すなわち一定の温度にある熱源からは仕事を生み出すことができません。
ついでながら、この効率の式を眺めると、低温源と高温源の差が大きいほど \( \frac{T_{L}}{T_{H}} \) は小さな値となりますので、効率は大きくなることが分かります。また、具体的に効率を求めてみると、\(T_{H} = 373K \) (100℃)、\( T_{L} = 273K \) (0℃) の場合、\( \eta= \)27% ですから、73%のエネルギーは仕事、すなわち有効なエネルギーに戻すことはできないのです。
久々の水飲み鳥の登場です。水飲み鳥が第1種永久機関でないことはすでに説明しました。第2回の講義の課題で問いかけ、第5回の講義で説明したように、周囲から 流れ込む熱のエネルギーを使って動いています。

しかし、第2種永久機関にはならないのでしょうか?周りの空気はどこも同じ温度です。「一定の温度にある熱源から正の熱を取り出し」にあたるのではないでしょう か。水が低温源だと思われるかもしれませんが、第1種永久機関でないことの説明の中でも述べた通り、熱は必ず熱いものから冷たいものに流れますから、コップの 中の 水そのものの温度は空気と同じとなり、低温源とはいえません。ただし、われわれが水を冷たいと思うのは、多くの場合、水そのものの温度ではなく、水が蒸気となって 気化するときに、気化するのに必要なエネルギーをわれわれから奪うからなのです。気温の低いときにプールにはいると水の中の方が温かく感じるのは、水の中では 気化 熱を奪われないからですし、お風呂で浴槽から出たときに体にはお湯がついているのに寒く感じることがあるのは、気化熱を奪われるからです。結局、水飲み鳥は、頭部のフェル ト にしみ込んだ水そのものの温度ではなく、水が蒸発することで気化熱を奪われ、温度が下がり、腹部との間に温度差が生じているのです。
ちなみに、図6.6の右の写真のように、密閉された状態に置くと、水飲み鳥はやがて動かなくなります。頭部から気化した水蒸気が密閉された空間の湿度を 100%まで 押し上げると、もうそれ以上に水は気化することができず、温度差を生み出すことができないからです。 水飲み鳥は第1種永久機関でも第2種永久機関でもないことがこれで示されたわけですが、図6.6の2つの写真を見比べ、まだ何となくもやもやしたものが残るとしたら、 いよいよエントロピーの不思議にハマってきた証かもしれません。実は、左が開かれたシステム、開放系であるのに対して、右が閉じられたシステム、閉鎖系である という違いが重要な意味をもっているのですが、それを直感的に感じているからかもしれません。この点については、第10回の講義でふたたび水飲み鳥に登場いた だき、説明したいと思いま す。
エントロピーに関する本を読み進めると「宇宙の熱的な死」という言葉に出会います。熱という形になったエネルギーはそのすべてを再び仕事に変換できず、エ ネルギー はどんどん熱という形に変わっていってしまい、最後にはこの宇宙はすべて熱となり、死を迎えるというわけです。しかし、熱というエネルギーの形はどことなく漠 然としていて、何かこの説明はしっくりきません。私的には次のように考えて理解しています。 熱を仕事に変えるには高温源と低温源が必要です。高温源から熱を奪えば高温源は温度が下がり、低温源に熱を捨てれば低温源の温度が上がります。こうして宇宙のすべ ての温度が一様な温度になる方向へと向かって進んでいきます。そうして、すべての温度が一様になったとき、すなわち、どこにも温度差がない状態になったとき、 もはや 仕事を生み出すことはできず、宇宙は死に至るということです。もちろん、それは皆さんが生きている時間よりはとてつもなく長い時間であり、杞憂ではあるのですが、 局所的には、さまざまな意味で「差」が消えていくことで秩序が崩壊していくことが起こり得るのです。これについては、残りの講義の中で、少しずつ論じられるこ とになります。 今回はここまでにします。次回へと続きます。

可逆熱機関における熱源の温度 \(T_{H}\)、\(T_{L}\)と熱 \(Q_{H}\)、\(Q_{L}\)の関係