トップページ　＜　エントロピー・多様 性・複雑系　＜　カルノーサイクル（１）＜　可逆機関におけ る熱源の温度と熱の関係

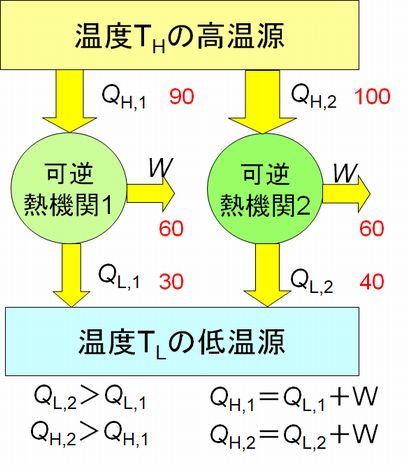
　ここでは、可逆熱機関における熱源の温度 \(T_{H}\)、\(T_{L}\) と熱 \(Q_{H}\)、\(Q_{L}\) の関係を求めます。そのため、まず、効率の異なる2種類の可逆機関は存在し得ないことを証明します。すなわち、可逆機関であれば、その機関の仕組みに関係なく、一意的に \(T_{H}\)、\(T_{L}\) と熱 \(Q_{H}\)、\(Q_{L}\) の関係が定まることを確認します。

　左図には、そのメカニズムが異なり、効率の異なる２つの可逆熱機関が示されています。いま、可逆熱機関２の方が１より効率が悪いとします。すなわち、同じ \(W\) の仕事を生み出すのにより多くの熱エネルギーを高温の熱源から得なければならないとします（すなわち、\(Q_{H,2} \gt Q_{H,1}\)）。そして、証明です が、第6回講義の中で行ったように、効率の悪い可逆熱機関２を逆回転したものを、より効率のよい可逆熱機関１に接続します。すると可逆熱機関１で作られた仕事 \(W\) をすべて使って、逆の可逆熱機関２は、熱を低温源から高温源へと運びますが、可逆熱機関１が高温源から低温源へと運ぶ熱と差し引きすると、\(Q_{H,2} - Q_{H,1} \gt 0\)、\(Q_{L,2}-Q_{L,1} \gt 0\) 、すなわち低温源から高温源へと実質熱が流れることになります。これはクラウジウスの原理に反しますので、結局、効率の異なる可逆熱機関が存在することはあり得ないことに なります。このことは、また、高温源の温度と低温源の温度が決まると、可逆熱機関の効率は一意的に決まることを意味しています。

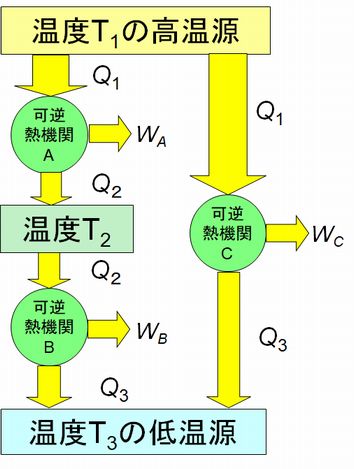
　左図のように、可逆熱機関Aと可逆熱機関Bを、高温源と低温源の中間の温度の熱源を介して接続することを考えます（\(T_{1} \gt T_{2} \gt T_{3} \)）。このAとBを 組み合わせた ものも一つの可逆熱機関とみなすこともできますから、それを可逆熱機関Cとして表したものが左図の右側の部分です。

　効率は　\( \eta = \frac{W}{Q_{H}} = \frac{Q_{H} – Q_{L}}{Q_{H}} = 1 – \frac{Q_{L}}{Q_{H}} \) で与えられますから、\( \frac{Q_{L}}{Q_{H}} \) について考えると、これが高温源の温度と低温源の温度で決まるということは、その関数であるということになります。すなわち、

\[ \frac{Q_{1}}{Q_{2}} = f (T_{1}, T_{2}) 、 \frac{Q_{2}}{Q_{3}} = f (T_{2}, T_{3}) 、 \frac{Q_{1}}{Q_{3}} = f (T_{1}, T_{3}) \]
となります。ここで　  \( \frac{Q_{1}}{Q_{3}} = \frac{Q_{1}}{Q_{2}} \, \frac{Q_{2}}{Q_{3}} \)　　より
　　\[ f (T_{1}, T_{3}) = f (T_{1}, T_{2}) f (T_{2}, T_{3}) \]
が導かれます。これを満たすためには、関数 \(f\) は次の形をとる必要があります。
　　　\[ f (T_{1}, T_{2}) = \frac{\phi (T_{1})}{ \phi (T_{2})} \]
\( \phi \) の関数形はこれでは定まりませんが、もっとも単純なものとして　\( \phi (T) = T \) を採用すれば、
　　   \[ \frac{Q_{1}}{Q_{2}} = f (T_{1}, T_{2}) = \frac{T_{1}}{T_{2}} \]
となり、\[ \frac{Q_{1}}{T_{1}}=\frac{Q_{2}}{T_{2}} \] が導かれます。