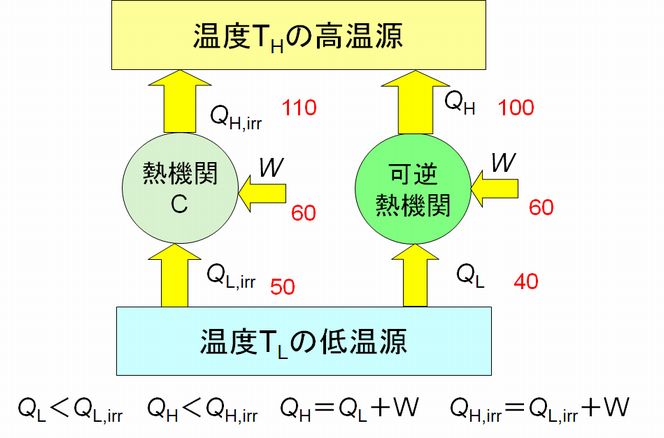
図7.1 逆回転した熱機関Cと逆のカルノーサイクル
今回はいよいよエントロピーが定義されます。この講義もすでに6回を終えましたが、やっとたどり着いたという感じです。そして、エントロピー増大の法則が証明さ れます。
まずは、前回の講義で残された問題からはじめます。それは、逆のカルノーサイクルも一般の熱機関の逆サイクルよりも効率がよい、という証明です。
図7.1に示すように、熱機関Cは逆回転すると逆のカルノーサイクルよりも効率の良い熱機関として働くと仮定します。これらは、クーラーと同じような熱機関ですので、熱 機関Cは同じ仕事（電気量）Wでより多くの熱を低温源から奪い取ることができるというわけです。
これまで通り、カルノーサイクルと結合した組み合わせ熱機関を考えてみましょう（図7.2）。この組み合わせ熱機関は、外部からエネルギーを供給されるこ とな く、低温 源から高温源へと熱を運んでいます。エネルギーを必要としないクーラーが実現してしまいました。これはあり得ない。きちんと表現すれば、クラウジウスの原理に 反す るわけで、カルノーサイクルが理論的に存在可能ですから、熱機関Cが存在すると仮定したことが過ちだったということになります。結果、熱機関C、すなわち逆のカルノーサイ クルより効率のよい逆サイクルをもつ熱機関は存在しないことが証明された、というわけです。
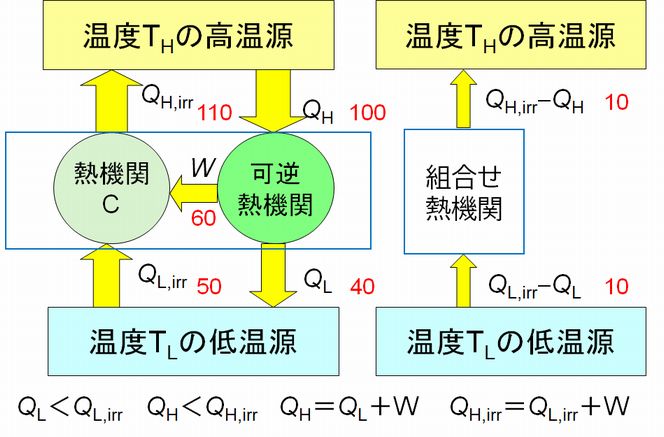
前回の講義内容も含め、以上のことをまとめると以下の通りです（図7.3参照）。
① カルノーサイクルは可逆熱機関であり、
\[ \frac{Q_{H}}{T_{H}}=\frac{Q_{L}}{T_{L}} \tag{1} \]
が成り立ちます。また、その効率は \( \ \eta= \frac{W}{Q_{H}}=\frac{Q_{H}-Q_{L}}{Q_{H}}=1-\frac{Q_{L}}{Q_{H}}=1-\frac{T_{L}}{T_{H}} \) となりま す。
② 熱機関Xは、可逆の熱機関であるならば、\( \frac{Q_{H}}{T_{H}}=\frac{Q_{L}}{T_{L}} = \frac{Q_{H,g}}{T_{H}}=\frac{Q_{L,g}}{T_{L}} = \frac{{Q^\ast}_{H,g}}{T_{H}}=\frac{{Q^\ast}_{L,g}}{T_{L}} \) が成り立ちます。Xがカルノーサイクルとは全く異なる仕様の熱機関でも、可逆であればこの関係式は成り立ちます。したがって、効率もカルノーサイクルとまったく同じです。
③ 熱機関Xがカルノーサイクル（図7.3中央）より効率が悪いとき、仕事を外部にする場合（図7.3左端）と外部から仕事をされる場合（図7.3右端）とを分けて考える 必要 があります。 外部に仕事をする場合、熱機関Xの効率は \( \eta_{X}=1-\frac{Q_{L,g}}{Q_{H,g}} \) ですから、\( {\eta}_{X} \lt \eta \) より \( \frac{Q_{L,g}}{Q_{H,g}} \gt \frac{Q_{L}}{Q_{H}} \) となります。さらに \( \frac{Q_{L}}{Q_{H}}=\frac{T_{L}}{T_{H}} \) より \( \frac{Q_{L,g}}{Q_{H,g}} \gt \frac{T_{L}}{T_{H}} \) すなわち
\[ \frac{Q_{L,g}}{T_{L}} \gt \frac{Q_{H,g}}{T_{H}} \tag{2} \]
となります。 外部から仕事をされる場合は、効率 \( \eta _{X} \)、\(η\) は小さいほど少ない仕事 \(W\) でより多くの熱を高温源に流すことができるため、\( {\eta}_{X} \)、\( \eta \) が小さいほど効率がよいことになりま す。したがって、\( \frac{{Q^\ast}_{L,g}}{{Q^\ast}_{H,g}} \lt \frac{Q_{L}}{Q_{H}} \) であり、\( \frac{Q_{L}}{Q_{H}}=\frac{T_{L}}{T_{H}} \) を使えば
\[ \frac{{Q^\ast}_{L,g}}{T_{L}} \lt \frac{{Q^\ast}_{H,g}}{T_{H}} \tag{3} \]
となります。
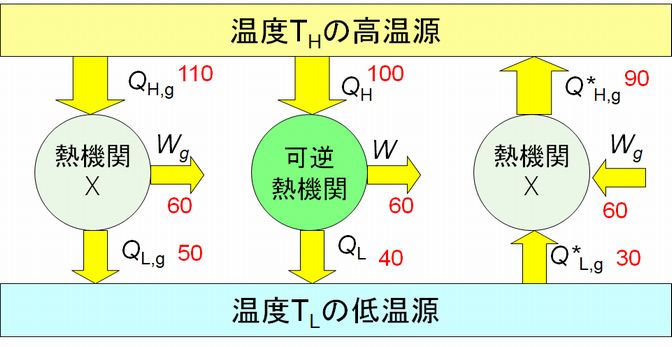
ここまでの議論で \( \frac{Q_{L}}{T_{L}}\ \) や \( \frac{Q_{H}}{T_{H}} \) という量が最終的な結論の式(1)、(2)、(3)に現れていることにお気づきでしょうか。熱を、それが流れ出た熱源の温度で割る、あるいは、熱をそれが流れ込んだ熱源の 温度 で割るという形をしています。そこで、これを新たに \(S\) と置くことにします。さらに、熱機関に入力するときの \(S\) を \( S(入力)\)、熱機関から出力するときの \(S\) を \(S(出力)\) とすると、式(1)は \(S(入力) = S(出力)\) と書け、式(2)、(3)はどちらも \(S(入力) \lt S(出力)\) と書くことができます。そして、実は、この \(S\) こそ、エントロピーなのです。 そろそろ議論についてこれなくなったかもしれませんが、もう少し先に進みましょう。結論は、とにかくエントロピーは増大する（正確には、減少しない）ということで、それを 証明しようとしているということだけは認識して読み進んでください。
可逆熱機関の内部（図7.3の可逆熱機関と書かれた円の中）では熱の出入りを受け、状態が変化しながら、また元の状態に戻るというサイクルが行われていま す。その変遷 する状態の中から、いま２つの状態AとBを取り上げてみることにします（図7.4）。カルノーサイクルでいえば、高温源と同じ温度で、もっとも体積が小さい状態を 状態 A、もっとも体積が大きくなった状態を状態Bとするといったところです。状態Aから状態Bへは温度 \(T_{1} \) の高温源から熱 \(Q^{\ast}_{in} \) を受け取り体積を膨張させます（等温膨張）。状態Bから状態Aへは、断熱膨張を経て、温度 \(T_{2} \) の低温源に熱 \( Q^{\ast}_{out} \) を捨て体積を減少させ（等温圧縮）、さらに断熱圧縮を経て状態Aに戻ります。 このとき、\( \frac{{Q^\ast}_{in}}{T_{1}}=\frac{{Q^\ast}_{out}}{T_{2}} \) が成り立つというのが上の議論でした。そこで、このエントロピーという量は、それぞれの状態で決まった量として定義でき、すなわち状態Aのエントロピーは \(S_{A} \)、状態Bのエントロピーは \(S_{B} \) というように定義でき、その差 \( S_{B} －S_{A} \) が \( \frac{{Q^\ast}_{in}}{T_{1}}=\frac{{Q^\ast}_{out}}{T_{2}} \) に等しいと考えてみたらどうだろうというわけです。
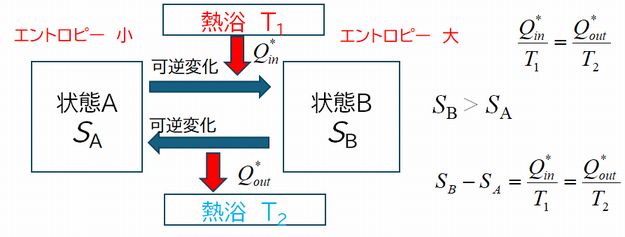
図7.4の図式は、あくまで可逆熱機関の中で成立しています。そこで、状態Aから状態B、あるいは状態Bから状態Aへのどちらか一方の変化が可逆でない、 すなわち不可逆変化である場合を考えてみましょう（図7.5参照；これが図7.3の熱機関Xと書かれた円の中身と考えます）。ただし、\(S_{B} \gt S_{A} \) とします（\(S_{B} \lt S_{A} \) と仮定しても同じ結論に達します）。\( S(入力) \lt S(出力) \) でしたので、[case 1] では \( \frac{Q_{in}}{T_{1}} \lt \frac{{Q^\ast}_{out}}{T_{2}} \) 、[case 2] では \( \frac{{Q^\ast}_{in}}{T_{1}} \lt \frac{Q_{out}}{T_{2}} \) となります。\( \frac{{Q^\ast}_{in}}{T_{1}}=\frac{{Q^\ast}_{out}}{T_{2}}=S_{B}-S_{A} \) をこれに代入すると、 [case 1] では \( \frac{Q_{in}}{T_{1}} \lt S_{B}-S_{A} \)、[case 2]では \( S_{B}-S_{A} \lt \frac{Q_{out}}{T_{2}} \) となります。ここで \(Q_{in} \) あるいは \(Q_{out} \) を 0 としてみます。すると [case=1] では \( S_{B}-S_{A} \gt 0 \) すなわち \( S_{B} \gt S_{A} \) となり最初の仮定に矛盾しませんが、[case 2] では \( S_{B}-S_{A} \lt 0 \)、すなわち \( S_{B} \lt S_{A} \) となり、最初の仮定 \( S_{B} \gt S_{A} \) と矛盾します。したがって、[case 2] は起こり得ないことになります。
整理しましょう。\(Q_{in}\) あるいは \(Q_{out}\) を 0 と置いたのは熱の出入りがない状況を想定したことに相当します。そうした場合、[case 1] のように状態Aから状態Bへの変化は可能であるが、[case 2] のように状態Bから状態Aへの変化は起こることができないと結論されたということです。\(S_{B} \gt S_{A} \) でしたので、[case 1] はエントロピーが増大する変化、そして[case 2] はエントロピーが減少する変化です。結局、熱の出入りがない状態での変化は、エントロピーが増大する方向は可能であるが、その逆、すなわち減少する方向には起こり得ないこ とが証明されました。言い換えれば、熱の出入りがない状態で変化が起これば、エントロピーは必ず増加することになるのです。
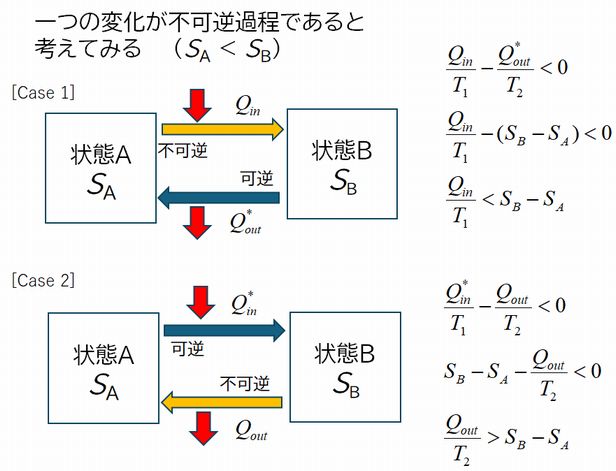
結局、「体系が断熱壁に囲まれているとき、不可逆変化が起こればエントロピーは必ず増加する。ただし、可逆変化ではエントロピーは変化しない。」 ことが証明されたわけです。これがエントロピー増大の法則です。（可逆変化ではエントロピーは変化しないので、正確にはエントロピーは減少しない、です。）
熱機関という非常に限定されたモデルからスタートした議論から、突然、エントロピー増大の法則の証明に大変身してしまい戸惑っているかと思いま す。 何でそんな離れ業ができたのでしょうか。
カルノーサイクルを使って、一般の熱機関はカルノーサイクルの効率を超えることができないことが証明されました。それまで、より効率のよい熱機関を、と
頑張っていろいろ考えていたわけですが、この時点で、一般の熱機関として、カルノーサイクルの効率を超えることができないものの比較的効率の良いものか
ら、どうしようもない役立たずのものまで幅広く捉えられるようになりました。さらにその考えを拡張すれば、熱機関と呼べないようなものでもどうしようもな
い役立たずの一般の熱機関としてその範疇に含むことができるわけですから、自然現象をすべてこの一般の熱機関と捉えることもできると発想の大転換を行った
わけです。同じ対象に２つの状態AとBがあって、状態Aから状態Bへ、そして再び状態Bから状態Aというサイクルを考えたとき、そのすべてにこの議論が成
り立つわけです。実際には、さらに一般性を高めるための議論を展開する必要があるのですが、もはやこの講義の範囲を超えています。とにかく、自然現象すべ
てに対して成り立つ法則としてのエントロピー増大の法則が、こんな感じで証明された、という雰囲気だけでも味わっていただければ幸いです。
エントロピーは物理的には状態量の一つとされます。状態量とは、体積、質量、圧力、温度、濃度など、考えている系に対して一意的に定まり、その状態にな るのにどのような経緯を経たかなどの過去の履歴に依存しない量をいいます。そしてこれまでの説明にありましたように、状態Aから状態Bに可逆過程で遷移す るときの \( \frac{Q_{A \rightarrow B}}{T_{1}}\) と、状態Bから状態Aに可逆過程で遷移するときの \( \frac{Q_{B\rightarrow A}}{T_{2}} \) とが等しいことから、２つの状態のエントロピー差は\( S_{B}-S_{A}= \frac{Q_{A \rightarrow B}}{T_{1}}=\frac{Q_{B \rightarrow A}}{T_{2}} \) であると定義されています。すなわち、エントロピーは可逆変化で定義される量であることに注意してください。この点を例を使って説明します。
ある状態から他のある状態へと至る経路は一般に複数存在し、可逆過程と不可逆過程に分類することができます。そして２つの状態のエントロピー差は、可逆 過程における熱の出入りによって定義されます。図7.6を使って説明しましょう。
図7.6の上の図の左右どちらも、気体の体積、温度、圧力などすべて等しく、したがってエントロピーの値も等しく、下の図の左右についても同様とし ます。しかし、左の図では、温度 \(T\) 一定の等温膨張により上から下の状態へ、逆に等温圧縮により下から上の状態へと遷移していて、そのときの出力熱量 \( Q_{1→2} \) と入力熱量 \(Q_{2→1} \) が等しい（（\(Q_{1→2} = Q_{2→1} = Q \) ）可逆過程となっています。したがって、２つの状態のエントロピー差は \( S_{2}-S_{1}= \frac{Q_{1 \rightarrow 2}}{T}= \frac{Q_{2 \rightarrow 1}}{T}= \frac{Q} {T} \) と定義できるわけです。
一方、図7.6の右では、上の図で気体
と真空の部屋を隔てている壁を取り除くことで下の状態へと遷移しており、それに対応する逆の過程が存在しない不可逆過
程です。しかも熱の出入りがありません。したがって、こうした不可逆過程を考慮しても、そこから２つの状態のエントロピー差を計算で求めることはできないのです。
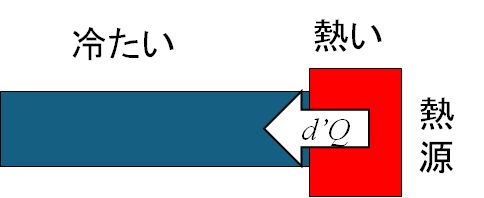ところで、等温的な可逆変化で気になることがあります。熱は温度差のあるところを流れます。したがって、熱源からピストンに対して熱が流れるためには そ
こに温度差があることが必要です。しかし、温度差があるところを熱が流れると、エントロピーは (熱)/(温度)
で定義されていますから、同じ熱量が高温側から低温側に流れても、流れ出たエントロピーと流入したエントロピーは等しくなく、後者の方が大きくなります。
\( dS_{低温} = \frac{d'Q}{T_{低温}}
\gt dS_{高温} = \frac{d'Q}{T_{高温}} \)
可逆変化では、両者は等しいはずですから、これは困ります。すなわち、温度差がなければ熱が流れないけど、温度差があればエントロピーは増大してしまう、あ るいは不可逆過程がそこに生じてしまうというジレンマに陥ります。
そこで、高温側と低温側の温度差は無限に小さいとし、実質等しいとして扱います。そのとき流れる熱量も無限に小さくなるため、 \( d’Q \) と表現します。\(d\)に付け られた「’」はとりあえず飾りくらいに思っておいてください。そして、教科書でエントロピーの定義を見ると次のように書かれています。
絶対温度 \(T\) での準静的等温変化で微小熱量 \(d’Q\) を吸収したときの系のエントロピーの増加 \(dS\) は
\[dS= \frac{d'Q}{T} \]
で与えられる。
微分積分を学習した人は \(d\) のついた無限小量のもつ意味がわかるかと思います。これは数学的テクニックで何か騙されている気がするかもしれませんが、温度差によ るエントロピー増加を抑え、入力側と出力側のエントロピーの変化を等しくしながらの等温変化を可能とするのです。
ただ、これを満たすように実際にピストンを動かすとしたら、無限の時間をかけてゆっくり動かす必要があります。ほとんど動いていないけど、動いているとい
う状
態で、これを「準静的変化」とよんでいます。結局、カルノーサイクルは最高効率の熱機関なのですが、それを実現するためには無限にゆっくり動かす必要がある、
ということで、理論的には可能だが、まったく実用的でない熱機関ということになります。したがって、身の回りにはカルノーサイクルで動く熱機関はありません。
すなわち、実在するすべての熱機関は、カルノーサイクルより効率が悪く、ということは、入力のエントロピーより、出力のエントロピーが大きくなり、結果として
エントロピーを増大させていることを示しています。
今回は難しい議論でしたし、詳細を省略した部分もあって論理に飛躍があるように感じられた方もおられると思いますが、実際は、緻密に組み立てられた論理に よってエントロピー増大の法則が証明されています。前回の冒頭に述べましたように、こうした証明を掲げたのは、物理科学的な論理の進め方に少しでも触れていた だ こうと思ったためで、これが理解できなかったとしても、今後の話についていけないということではありませんので安心してください。兎にも角にも、こんな感じで エントロピー増大の法則が自然界のあらゆる現象に適用できる法則であることが証明されています。みなさんにとって大切なことは、それでは「それがどうした」と いう点かと思います。そのためにはもう少し、「エントロピーとは何か」をどのようにイメージしたらいいのかお話しする必要があるかと思います。次回は、そんな ところから話を進めたいと思います。