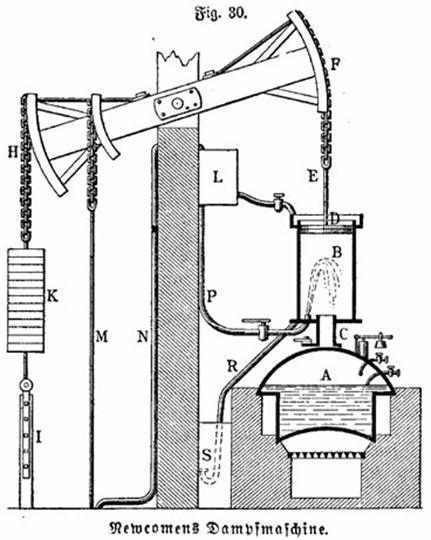
図5.1 ニューコメンの蒸気機関
これから4回にわたってカルノーサイクルという熱機関のお話をします。熱機関とは、熱を使って仕事を得る ための機械で、もっとも典型的なものは蒸気機関でしょう。なお、ここでいう「仕事」は、これまでにもたびたび出てきましたが、ちゃんとした物理学用語で、熱機関が 外部に対して生み出す、あるいは外部からその熱機関に対して投入する力学的なエネルギーを指しています。まあ、これからこの言葉が出てきたら、一般性は失いま す が、「電気エネルギー」をイメージし、外部に対して仕事をする場合には「発電をする」、外部から仕事をする場合には「電力を消費して動かす」に言葉を置き換えると わかりやすいかもしれません。 なぜ熱機関の話をするかというと、蒸気機関の改良を考えていく過程で、カルノーという研究者が、熱というエネルギーをすべて仕事に変換することができないことを証 明してしまい、それがエントロピーという概念が生まれる契機となったからです。
第2回の講義で、エネルギーにはいろいろな種類があり、相互に可換であり、変換に よってエネルギーの量は変わらないことを説明しました。しかし実際には、この可換であるという表現には例外があったのです。そして、エネルギー保 存の法則が成り立つのになぜエネルギーを節約しなければならないかという問いの答えが、まさに、この熱というエネルギーをすべて仕事には変換できない、ということが ポイ ントだったのです。前回、エネルギーの質の劣化の話をしました。風車の話は多くの方がイメージを抱きやすかったと思いますが、あくまで一つの例であり、これだけ であらゆるエネルギーについて、その質の劣化を論じることはできません。それをより一般的な議論へと拡張するため、これから話をすることになります。
今回のカルノーサイクルの説明は非常に具体性をもった話ですが、次回からは非常に概念的で、捉えどころが難しいと感じられるかもしれません。しかも、エン トロピー はあらゆる自然現象に適用される法則のはずが、熱機関という特殊なものにこんなに固執した議論をしていていいのかと思われるかもしれません。しかし、最後に 話が 突然大きく展開します。その論理展開の醍醐味が非常に自然科学的なので、わざわざ4回にもわたって講義をしようと思いました。難解で面白味に欠けるかもしれませんが、その 論理を 楽しめるよう理解に努めてみてください。
カルノーサイクルの説明に入る前に、熱機関の典型例である蒸気機関の歴史を少しだけお話しします。しかしあくまでも話の枕ですので、雑学を勉強する気分で、また ウォーミングアップと思って気軽に読んでください。
(1) ニューコメンの蒸気機関
ニューコメン(1664-1729年)は、イギリスの発明家、技術者であり、鉱石の採掘の際に出る水を排水するために、最初の実用的な蒸気機関を建造しました。 その後の産業革命の動力を担った蒸気機関の実質上の発明者とされています。 図5.1にニューコメンの機関の概要を示しました。

基本構造は蒸気を生み出すボイラー(A)、蒸気を閉じ込めたシリンダー(B)、そして上下するピストン(D)から成りま す。シリンダーの下端には蒸気の入口(C)だけではなく、冷水の噴射口があるのが特徴です。ボイラーから入ってきた蒸気で膨張しているシリンダー内に冷水を噴 射す ると、中の蒸気が凝縮し、シリンダー内の気圧が一気に下がります。これにより大気圧がピストンを下へと押し下げ、ピストンを鎖で吊っているビーム(大きなてこ)の一 端を引き下げて、ビームの他端から吊り下げたロッドを介して、坑道底の容器で水を汲み上げる、というわけです。蒸気がシリンダー内に充満していくときに は何も 仕事をせず、水を汲み上げるという仕事は大気の力で行われていますので、正確には蒸気機関とは言えないかもしれません。最後に、蒸気入口の弁を開くと下のボイラーか ら再び蒸気が注入され、シリンダーは再び上へと押し上げられ、同じ工程が繰り返されます。
(2) ワットの蒸気機関
ニューコメンの機関は、蒸気で温まったシリンダー内を冷水で冷やしてしまいます。したがって、再び蒸気がシリンダー内に入ったとき、蒸気がシリンダーを温 めること にも使われてしまうため効率が悪く、多量の石炭を必要としました。イギリスのジェームズ・ワット(1736-1819)は、グラスゴー大学に勤務中に修理を依頼さ れたことから、ニューコメン機関のこの欠点に気づき、1765年、蒸気をシリンダーとは別の容器に導いて冷やして水にする復水器という装置をつくることで 、ニューコ メン機関の4倍程度の効率をもつ機関へと改良し、広く使用されるようになりました。
ワットの蒸気機関の動作原理を図5.2に沿って説明しましょう。

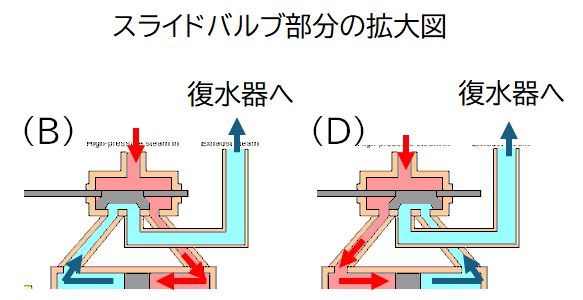
(A)→(B)→(C)
シリンダーの右側に高温・高圧の蒸気が導入されます(赤で塗られた部分)。シリンダーの左側にあった前工程で導入された蒸気(水色で塗られた部分)は、上部にあるスライ
ド バ
ルブを通って外部にある復水器へと押し出されます。復水器で蒸気は冷却され凝縮するため、シリンダーの左側の圧力は急激に低下し、右側にある高温・高圧の蒸気
に よってピストンは右から左へ勢いよく動くことができます。
(D)→(E)
スライドバルブはピストンの運動と連動して動き、蒸気の通り道を変更します。今度はピストンの左側から高温・高圧の蒸気が導入され、今度は工程
(A)→(B)→(C) で導入された右側の蒸気がスライドバルブを通って復水器へと排出され、ピストンは左から右へと動き、これが繰り返されます。
ピストンの往復運動を回転運動に変化する機構や 、運転速度を一定に保つ調速器などもワットは開発し、用途が飛躍的に広がりました。
(注) ワットの蒸気機関のアニメーションが Wikimedia Commons
の以下のサイトにもあります。
https://commons.wikimedia.org/wiki/File:Steam_engine_in_action.gif
実は、ニューコメンの機関とワットの機関の作動原理の詳細は、この講義にとってはそれほど重要ではありません。ただ一つだけ注目しておいてほしいポイント があります。そ れは、どちらも蒸気を冷やす部分がシステムの中に存在していることです。ニューコメンはシリンダーの中で蒸気を冷やしました。ワットはそれが効率を悪くしていると 考え、シリンダーの外に復水器を設置し、そこで冷やすことで効率をあげました。しかし、それでも、燃料を使って折角作り出した高温の蒸気を冷やし、単なる水に 戻し てしまうと いう、 何とももったいない工程が含まれているのです。この無駄な工程を何とかなくすことはできないだろうか。これがカルノーが一生懸命考えたことでした。
この講義では、この冷 却部分があることが重要なポイントとなるのですが、ワットの蒸気機関について書かれたものを見ると、復水器について、文章では触れられているものの、図の中に 書き 込んであるものはほとんどありませんでした。われわれは、太陽エネルギーの恩恵を受けていることは誰もが実感していますが、それと同量のエネルギーを赤外線の形で 宇宙空間に捨てていることにあまり関心をもちません。われわれは、食事からエネルギーを摂取することの重要性を強く感じていますが、排泄や体表からの放熱の重 要性にはそれほどには関心がありません。原子力発電所がわれわれの文明を支えていることは十分に理解していますが、そこから出る核のゴミの取り扱いをどうする かといった問題にはほとんど無関心で す。こうした「捨てる」ということの重要性をこの講義の最後に理解していただくことが、この講義の目的の一つです。
カルノー(1796-1832)は、フランスの軍人、物理学者、技術者で、1824年、『火の動力、および、この動力を発生させるに適した機関についての 考察』を 著し、これが後にエントロピー増大の法則を生みだすことへと繋がります。この書で用いられた熱機関のモデルが、後にカルノーサイクルとよばれるもので、エントロピー 増大の法則の証明には欠かせないものとなっています。
図5.3に沿って、カルノーサイクルの説明をしましょう。
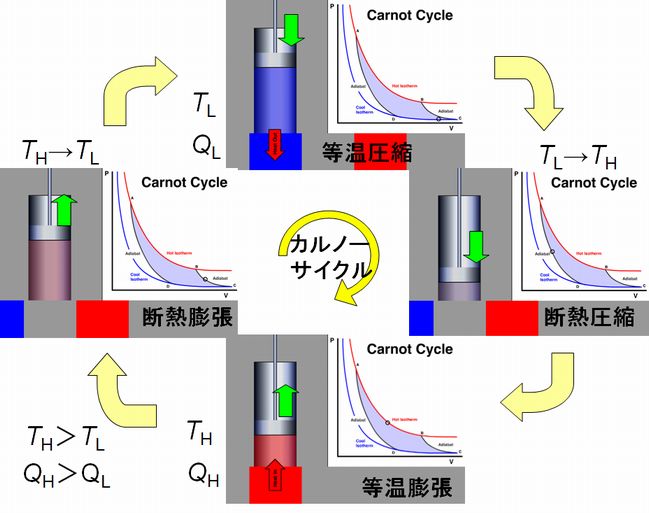
カルノーサイクルはシリンダーとピストンからなり、シリンダーは外部の熱浴と接しています。このとき高温の熱浴(図の赤色の四角部分で、その温度は \(T_{H}\))は シリン ダー内に熱を供給するために用いられ、低温の熱浴(青色の四角部分で、その温度は \(T_{L}\) )はシリンダー内の熱が流れ出る受け手として用いられます。また、シリンダー が外部と熱の出し入れを行わない断熱状態(図の灰色の部分がシリンダーに接しているとき)も設定されています。 カルノーサイクルは次の4つの工程から成り立ちます。
A. 等温膨張 第3回講義でお話ししたように、シリンダー内の気体分子は常に運動しており、壁に圧力をかけています。そして、可動なピストンに衝突するとその圧力が外部からの負荷を上 回ればピストンを外に押し出すことになります。しかし膨張するとき外部に対して仕事をすることになりますので、気体は運動エネルギーを減少させます。温度は運 動エ ネルギーに比例しましたから、気体の温度は下がることになります。このとき、高温の熱浴(シリンダーの外にある赤色の四角)に接し、外部から熱がシリンダー内に流 入できるようにしておけば、その熱浴と同じ温度になるまで自然と熱がシリンダー内に流れ込みます。ゆっくりとピストンを動かせば、熱浴とピストンの間にほとん ど温度差が生じることなく、すなわち、シリンダー内を高温の熱浴と同じ一定温度に保ったまま、膨張させることができます(この点については、後にまた触れるこ とになります)。これを等温膨張といいます。 なお、このときシリンダー内の温度を \(T_{H}\)、シリンダー内に流れ込んだ熱の総量は \(Q_{H}\) とします。
B. 断熱膨張 ある程度膨張が進んだところで、高温の熱浴を外し、シリンダー内を断熱状態に置きます。この状態でも外部からの負荷が小さければ気体は膨張を続けることができます。 すなわち、外部に対して仕事をします。しかし、断熱状態ですので、膨張という仕事を行うことにともない気体の運動エネルギーは低下し、その温度は低下します。 これを断熱膨張といいます。 なお、このときシリンダー内の温度は \(T_{H}\) から \(T_{L}\) に変化します。しかし熱の出入りは当然ながら 0 となります。
C. 等温圧縮 シリンダー内の気体がある程度膨張し、温度が低温の熱浴の温度 \(T_{L}\) まで下がったところで、今度は気体を圧縮する工程に切り替えます。ここで断熱状態も取りやめ、低 温の熱浴(シリンダーの外にある青色の四角)をシリンダーに接触させます。このとき、この熱浴の温度もシリンダー内の気体の温度も等しく \(T_{L}\) です。 ピストンを気体の圧力に抗して圧縮するには力が要ります。すなわち、外部からシリンダー内の気体に対して仕事をする必要があります。気体は外部から仕事をされたこ とで、その運動エネルギーを増大させることになり、温度を上げることになります。しかし、ここで低温の熱浴と接していることで、そこに熱を流し出すことがで き、 シリンダー内の気体の温度を低温の熱浴と同じ一定温度に保つことができます。これを等温圧縮といいます。 このとき、シリンダー内の温度は \(T_{L}\)、シリンダー外へ流れ出た熱の総量は \(Q_{L}\) とします。
D. 断熱圧縮 ある程度圧縮が進んだところで低温の熱浴を外し、シリンダーを再び断熱状態に置きます。この状態でも外部からの仕事を続けると、シリンダー内の気体は体積を減少 させながら、その温度は上昇します。これが断熱圧縮です。気体の温度が高温の熱浴の温度 \(T_{H}\) と等しくなったところで、断熱状態を中断し、再び高温の熱源と接触させ、ステップAに戻ります。 このとき、シリンダー内の温度は \(T_{L}\) から \(T_{H}\) に変化しますが、この工程での熱の出入りは 0 です。 これがカルノーサイクルの1サイクルです。
カルノーサイクルが1サイクル行った段階での仕事量を考えてみましょう。等温膨張および断熱膨張のときには外に仕事をしています。これを利用すれば発電を行うこ とができます。一方、等温圧縮および断熱圧縮するときには外部から仕事をしなければなりません。すなわち、そのためには電気エネルギーを消費する必要がありま す。 発電で得られるエネルギーと消費するエネルギーを差し引いたとき、発電の方が大きくなければ、このサイクルは何の役にも立ちませんから、多分大きいだろうと予想は つきますが、調べてみましょう。
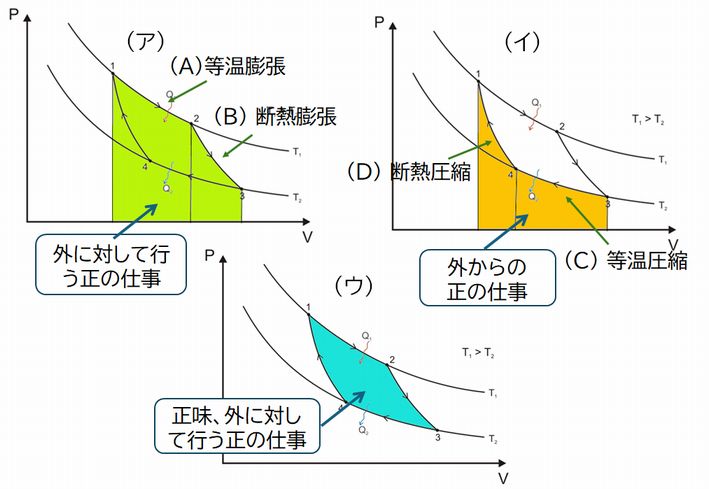
そのためには、第2回の講義でピストンの運動から仕事を計算するとき、\(PV\) 曲線(圧力の大きさを体積に対してプロットした曲線)を利用する方法を説明しましたが、それを使うのが便利です。それによれば、 \(PV\) 曲線においてある体積からある体積まで積分した値、すなわちPV曲線の下の部分の面積がその仕事に相当するというこ とでした。図5.4の(ア)では、(A)等温膨張から(B)断熱膨張までの外に対して仕事をしているときの仕事量が緑色で示した領域の面積に相当します。一方、(C)等 温圧縮から(D)断熱圧縮では外部から仕事をされるわけですが、(イ)における橙色で示した領域の面積がその仕事量に相当します。ここで、(A)(B)の \(PV\) 曲線 が(C)(D)の \(PV\) 曲線の上にあることが重要となります。その結果、緑色の領域の面積から橙色の領域の面積を引いた面積、すなわち(ウ)の水色の領域の面積が正 の値をもち、この面積に相当する仕事量が、カルノーサイクルの1サイクルで得られる正味の仕事となります。
ピストンを同じ温度で等温膨張、等温圧縮すれば、気体の運動エネルギーは等しいですから、外に対してする仕事も外からする仕事も等しくなりますが、等温圧縮する とき等温膨張したときより温度を下げることで、仕事に余剰が生まれたというわけです。
ところで、ニューコメンとワットの機関の説明において、高温の蒸気を冷却する部分があることに注目するよう指摘しましたが、このカルノーサイクルでもやはり高温の熱浴か ら得た熱の一部を低温の熱浴に捨 てています。高温の熱浴から熱 \(Q_{H}\) を得ても、それをすべて仕事に変換することができず、低温の熱浴へ熱 \(Q_{L}\) を捨て、その残り、\(Q_{H} - Q_{L}\) だけが仕事に変換されているのです。これでも何か改良されているのでしょうか。その答えは次回明らかとなります。
(注)この例では、等温膨張、断熱膨張だけを一発芸的に行うのであれば、熱をすべて仕事に変換する ことはできます。しかし、永続的に仕事を生み出すためには、元の状態にリセットし、繰り返す必要があります。すなわち、リセットするために外部からのエネル ギーが 必要となるのです。
カルノーサイクルの特徴の一つは、それが可逆の熱機関であるという点です。図5.3にある矢印をすべて逆向きに書いたのが図5.5ですが、これを逆のカ ルノーサイクルとよびます。ここで、\(T_{H}\)、\(T_{L}\)、\(Q_{H}\)、\(Q_{L}\) が、図5.3とまったく同じ値で動作することが可逆の意味となります。
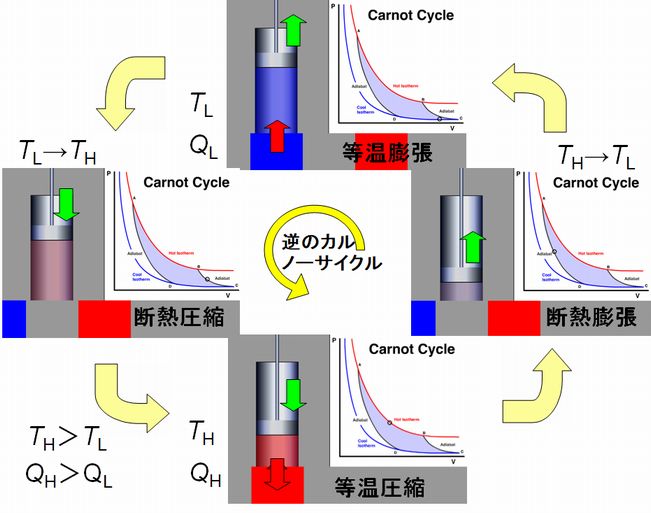
カルノーサイクルは、余剰の仕事を発電に振り向けることができましたが、この逆のカルノーサイクルでは、外からの仕事の方が大きくなりますから、エネルギーを消費す る機関です。それって何か意味のあることをするのでしょうか? 熱は低温の熱浴から奪い、高温の熱浴へと捨てています。低温の熱浴を冷蔵庫、高温の熱浴を室内、あるいは低温の熱浴を室内、高温の熱浴を外気とすれば、それぞれ冷 蔵庫とクーラーです。それぞれ電気のエネルギーを消費しないと機能しません。結局、逆のカルノーサイクルとは、エネルギーを消費しながら働く冷蔵庫であり、 クー ラーということになります。
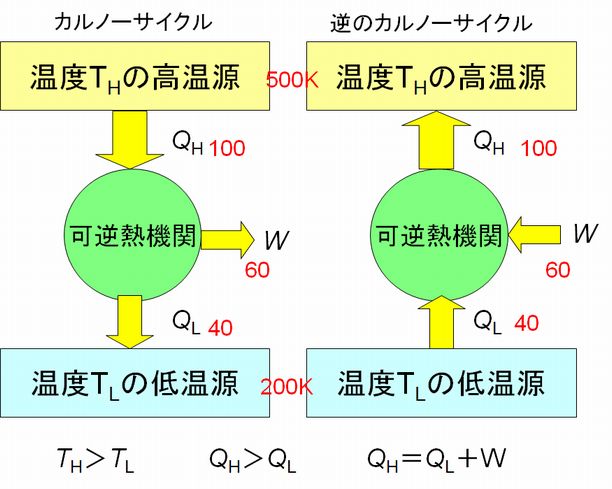
カルノーサイクルと逆のカルノーサイクルを、その内部構造を省略し、熱の出入りと仕事に注目してまとめると図5.6のように表現することができます。ここで \(W\) は正味の仕事を表しています。また、\(Q_{H} = Q_{L} + W\) はエネルギー保存の法則によるものです。
水飲み鳥の動作原理については、第2回の講義でお話ししました。しかし、その動作のエネルギー源については説明しませんでした。ここで、その答えをお話し しようと思います。
水飲み鳥の頭部はフェルトで覆われ、コップの水で濡れ、それが蒸発することで気化熱を奪われ、中の温度が下がります。これにより、中に封入されている気体 状態にあるジクロロメタンが凝集し、液化することで気体の圧力が下がり、液体のジクロロメタンが腹部から頭部へと上昇します。このとき、重心は腹部から頭部へ と移動し、頭をさげ、コップの水を飲むような姿勢となるというものでした。したがって、この水飲み鳥というシステムの温度が下がることになります(前にも注意 したように、コップの水が冷たいからではなく、気化熱が熱を奪うからです。コップの水は、周囲の温度と同じ温度になります。)。その結果、周囲と水飲み鳥との 間に温度差が生じます。そして、等しい温度になるべく、高温である周囲か ら、低温である水飲み鳥へと熱が流入することになります。

というわけで、この水飲み鳥というシステムに外部から流入するエネルギーはこの熱しか考えられませんので、この熱がエネルギー源ということになります。水 飲み鳥もりっぱな熱機関だったのです。当然ですが、エネルギー保存の法則に違反した、第1種永久機関ではなかったのです。
しかし、これで、水飲み鳥の問題は終わりというわけではありません。新たな疑問が、次回以降の話の中で生まれてきます。そこまで理解して、はじめて、この 玩具を理解できたと言えます。もうしばらく、楽しみにお待ちください。
今回の講義は、熱機関の仕組みが説明されましたが、結局、「だからどうしたの?」という問いには何も答えていません。でも、ここでちょっと一休みです。今 回はこれからの難解な話のためのあくまでもウォーミングアップ。この続きは次回に回しましょう。

断熱圧縮、断熱膨張 〜 フェーン現象とは