タンパク質の立体構造をコンピュータで研究するためには、まずはその立体構造をコンピュータ内で生成する必要がある。そのためには構成原子すべての位置座標を与える必要 があり、その総数 が系を記述する変数の数となる。化学結合長や結合角を固定し、化学結合の周りの回転角を独立変数とすることにより、変数の数を1/6ほどに減らすことができる が、それでも変数の数は数千におよぶこともある。さらに環境として存在する水分子も考慮するとなると、変数の数、自由度は一気に跳ね上がることになる。
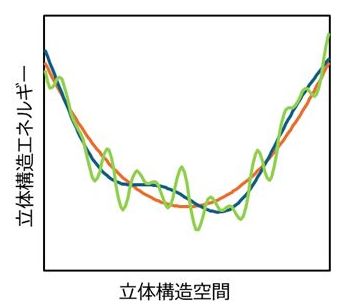
また、さまざまな立体構造は、その構造のポテンシャルエネルギー(立体構造エネルギーとよぶことにする)をその都度計算し、評価することが必要である。そのとき、原子 ペアごとに原子の種類、原子間距離、相互作用の種類などを考慮した計算が必要となり、その計算量も大きな問題となる。
この多自由度、相互作用の多様性がコンピュータによるタンパク質立体構造研究の特徴であり、それを実行するコンピュータのもつ計算資源(計算速度、記憶容量など)に大き く依存する点でもあ る。し かも、タンパク質ごとにアミノ酸配列が異なり、その天然構造も異なるため、得られた結果はそのタンパク質固有のものであり、タンパク質一般に成り立つような法 則をそこから導き出すためには、多くのタンパク質について計算を行う必要があり、きわめて難しいといわざるを得ない。
タンパク質の立体構造転移現象(再生↔変性現象)をコンピュータ内で実現するためには、構造空間内を網羅的にサンプリングすることが必要である。しかしそ れは、構造空間の広さ (次元の大きさ)を考えれば、どんな高性能のコンピュータが出現しても原理的に不可能であろう。そのため、アミノ酸残基を一つの球で表現するというモデルの粗視 化を行い、さらに2次元あるいは3次元の格子上のみを動くなどの仮定をおき、アクセスすべき構造空間に強い制約を課すなどの工夫が必要がある。さらに、天然構 造で相互作用する残基間のみ が空間的に隣接したとき相互作用するなどの近似(通称Goモデルと呼ばれる)を導入するなど、さまざまな工夫を凝らしながら研究が進められてきた。したがって、そうした研 究は、現実に存在する 具体的なタンパク質の物性を対象と した研究というよりも、タンパク質の立体構造転移の物理学的描像を得るためのモデル・シミュレーションという意味合いが強い。
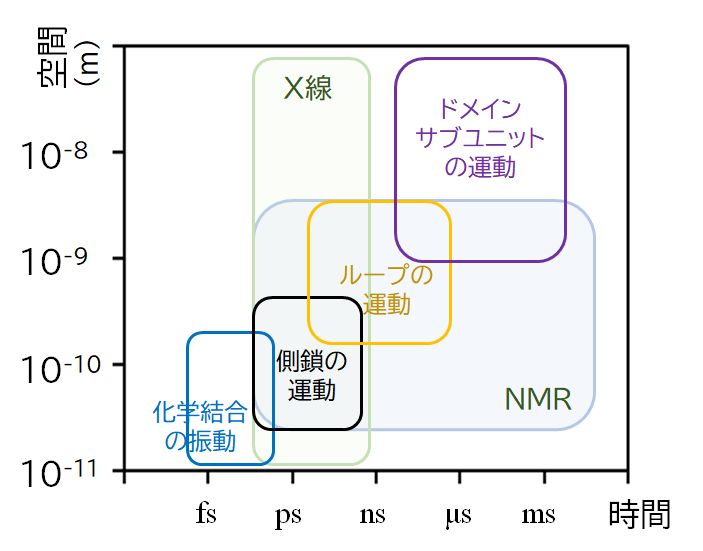
一方、現実のタンパク質を対象にした研究を行いたいと思えば、構造空間全域にわたるエネルギー地形を調べることは断念せざるを得ない。そんな状況でできることといえば、 天然構造近傍に限定したエネルギー地形の調査ということになる。その方法としては、基準振動解析(Normal mode analysis; NMA)、モンテカルロ(Monte Carlo; MC) シミュレーション、そして分子動力学(Molecular dynamics; MD)シミュレーションなどがある。なお、これらはタンパク質立体構造を対象とする研究に特化して開発された手法というわけではなく、広く、計算化学・計算物理学で用いら れてきた手法である。
基準振動解析は、系がエネルギー最小構造(天然構造)を頂点とする多次元の放物面の形をしたポテンシャルに束縛されていると仮定し、系の平衡状態における 振る舞い を解析的に計算してくれる。この方法は物性物理学などの分野で使われてきたものであるが、それをタンパク質立体構造のダイナミクス研究に初めて応用されたのは 1980年代初めのことである。
一方、MCやMDは、分子力学において得られているポテンシャル関数を使い、エネルギー最小構造(天然構造) 近傍の構造をサンプリングしながら、その都度その立体構造エネルギーを計算して評価し、構造空間の形状を調べる方法である。MCは ランダムサンプリングのため、非常にエネルギーの高い、すなわち現実には実現しないような構造もサンプリングし、立体構造エネルギーを計算した後、そのことを知って破棄す るといった過程が頻繁に起こるため、サンプリング効率が悪く、タンパク質の立体構造研究ではあまり利用されていない。これに対して、MDは、 ニュートンの運動方程式にしたがってサンプリングするためそうした無駄がないことなどから、現在ではもっとも広く利用されている。
基準振動解析は、立体構造エネルギー最小構造近傍を多次元の放物面で近似して得られる結果のため、その近似が有効な範囲、すなわち最小構造からあまり大きくずれない範囲 に関する情報のみしか得られないという制限がある。また、解析に先立ち、立体構造エネルギー極小の構造を準備する必要がある。一般に、PDBデータで提供され て いる立体構造は、分子力学で一般的に用いられているポテンシャル関数で計算した場合、必ずしもエネルギー極小構造とはなっていない。そのため、PDBの構造に最も近い立 体構造エネルギー極小の構造を計算で求める必要がある。しかも、精度高く極小点に到達していないと、基準振動解析で現れる行列の対角化で負の固有値が現れ、解 析の途中で現れるその固有値の平方根の計算ができず、解析が破綻することがある。そのため、タンパク質が大きくなると、その極小化に要する計算時間は解析に とって大きな負担 となる。こう した困難さはあるが、ひとたび精度よくエネルギー極小構造が得られると、基準振動解析は、行列の対角化というもっともコンピュータが得 意とする計算過程を経るだけで、きわめて手際よくタンパク質の運動を、そして構造空間の概要を手際よく描き出してくれる。
立体構造エネルギーの極小化は基準振動解析の一つのネックとなっていたが、後で述べるように、その必要のない新たな方法が出現したことで、基準振動解析はタンパク質立 体構造のダイナミクス研究において、もっとも簡便で、有用な方法の一つとなった。この点は、次に述べるMDが多くのシミュレーション時間を要するのに対して、 大き なメリットとなっている。したがって、多くのタンパク質に対して適用することを可能にし、その解析結果のデータベース化を可能にした。このWEBサイトで紹介 しているProModeはまさにそうした経緯で構築されたデータベースということができる。 残された問題は基準振動解析に課せられた近似の有効性が問題となるが、これについは後で触れることにする。
一方、MDは、適用できるのはやはり天然構造近傍の構造のサンプリングであるが、基準振動解析と比べるとはるかに広範囲におよび、しかもポテンシャル関数は分子力学など で吟味さ れてきた、より精度の高い関数形、パラメータ値が採用されており、基準振動解析に比べより信頼性が高い結果を出力する。基準振動解析に比して唯一の欠点は計算時間がかかる ことである。 しかし、コンピュータそのものの進歩により高速化、大容量化が進み、MDがカバーできる構造空間は急激に広がっており、構造空間の様相を解明する能力はますます 増強されている。
ただし、MDはあくまで構造空間のサンプリングを行うだけであり、そこで得られた生の出力データを見ただけで構造空間の様相をわれわれが理解できる形で描 いてくれるわけではない。以下に述べるように、そのデータを「解析する」ことが必要である点には注意しておく必要がある。
こうした生体高分子の構造やダイナミクス研究において、主成分分析(PCA: Principal component analysis)を基礎にした解析はもっとも基本的なアプローチの一つである。平衡状態において生成される立体構造の分布、すなわち構造空間の様相を調べる基準振動解 析、MDデータのエッセン シャル・ダイナミクス解析(EDA: Essential Dynamics Analysis)、特異値分解(SVD: Singular-value decomposition)などはすべてこのカテゴリーにはいる。PCAを基礎においたアプローチはどれも、見かけ上ランダムに見える天然構造周りの揺らぎ の中から生物学的な機能と直接関連のある多くのアミノ酸残基が協奏的に行う運動 (例えば、酵素の活性部位の開閉運動)を見事に導き出し、描き出してくれる。そして、そうした協奏的な運動はたいてい振動モード分布の中でもっとも低振動の領域に現れるこ とを示してきた。
物理的観点からすれば、低振動数モードは、エネルギー曲面の曲率が小さく、すなわちより平面に近いため、その方向にそって変形するともっとも低いエネル ギーでタンパク質全域にわたるような大きな変形を引き起こすことが可能であることを意味している(基準振動解析では、振動数の二乗はエネルギー地形における曲 率を意味しており、振動数が小さいと いうことは、その曲率が小さく、したがってもっとも柔らかいモードということができる)。
驚くことに、こうした低振動数モードの構造全域にわたる運動、それらはドメインのような大きな部分構造どうしの運動であるが、それは基準振動解析計算では、精密 な分子モデルか粗視化した分子モデルか、エネルギー関数の関数形やパラメータの値などにほとんどよらないことが示された。実際、粗視化モデルの先 駆的なTirionの研究(1996年)では、単一のパラメータで表現された仮想の力場による計算でも、分子力学に基礎をおいて設定された関数形とパラメータ値をもっ た力場による計算結果と、低振動数モードにおける構造全域にわたるような運動ではほとんど違いがみられなかった(より高振動数モードでの局所的な運動について は この 限りではない)。全域にわたる運動を支配しているのは残基間相互作用の ネットワークであるが、こうした事実からわれわれは、タンパク質立体構造のダイナミクスにはその幾何学的な性質が直接反映していると結論することができるであろう。
基準振動解析には、上で述べたようにいくつかの困難さがともなっていた。PDBで与えられた立体構造を初期値とした精度の高いエネルギー極小化が必要であること、基準振 動解析に課せられた近似のもとで、どの程度タンパク質立体構造のダイナミクスが正しく反映されるか、そしてその情報は、生命科学的に意義のある 結果をもたらすか、などである。しかしこうして粗視化したモデルでの基準振動解析の有用性が多くのタンパク質で示されるようになり、このホームページで紹介する 弾性ネットワークモデルによる基準振動解析のような研究が大きく進展し、その解析結果を収集したProModeのようなデータベースが構築されるようになっ た。
弾性ネットワークモデルによる基準振動解析では、各原子間がバネで結ばれているとして、そのポテンシャルを二次関数で与える。それゆえ「弾性」と呼ばれ、 さらに、すべて原子間に、あるいは各アミノ酸残基を一つの球で表すことも多く、その場合にはすべてのアミノ酸残基間にバネが張り巡らされ、ネットワークを構成 しているモデルということからこの名がついた。得られる結果のバネ定数への感受性は低いため、ある意味バネ定数は適当に決めることができる。そして最大のメ リット は、バネの自然長 を、PDBデータにおける原子間距離、あるいは粗視化モデルではアミノ酸残基間距離に設定できることである。これにより、PDBデータの立体構造をそのままエネルギー極小 構造とみ なすことができるようになり、 エネルギー極小作業を行う必要がなくなったのである。これにより、計算過程としては、行列の、ただし数千×数千次元の行列であるが、その対角化が唯一、コン ピュータの計算能力を必要とする部分となった。
最後に、タンパク質立体構造の基準振動解析が、その近似にも関わらず生命科学にとって意味ある結果を導きだしてくれるかは、その理論からは自明ではな い。それは、得られた結果から判断するしかないが、少なくともいくつかの例からは、その有用性が期待できることは確かである。CGで描きだされたタンパク質の ドメインレベルの相対運動を眺めていると、明らかにその機能と密接に関係していることを示唆しており、われわれからは何とも奇妙に見える立体構造の幾何学的様 相から、こうした運動が引き起こされるということに驚嘆せざるを得ない。こうしたCGを通した観察ではあるが、立体構造解析の次の一手へとつながっていくこと になれば、ProModeを作成した身としては大変あ りがたいことである。
DNAの塩基配列の情報がタンパク質のアミノ酸配列の情報をもち、アミノ酸配列の情報がタンパク質の立体構造の情報をもち、立体構造の情報が、その ダイナミクスの情報をもち、それがタンパク質の機能発現に重要な役割を果たしているという意味で、ここで述べてきたタンパク質立体構造がもつダイナミクスもま た、遺伝情報であるということができよう。したがって、タンパク質立体構造のダイナミクスもまた、進化の選択圧にさらされた結果であることを認識して調べてい く必要があり、そうした観点からの研究も、今後進められていくことを期待している。