前回の講義で、エントロピー増大の法則が証明されました。しかし、エントロピー増大の法則をそれで理解できたと思っている方はほとんどいないと思います。しか し、エントロピー増大の法則は、どうやら自然界で普遍的に成り立つ法則らしい、という点だけは認めておいてください。その上で、今回はエントロピー増大とは何 か、 感覚的に、より実践的にイメージを描くことを目指すことにします。
第3回の講義で分子の熱運動の話をし、第4回の講義でその分子の熱運動によって微視的状態数の少ない巨視的状態から微視的状態数の多い巨視的状態へと自然 と遷移 を引き起こし、その逆は確率的に起こらない、そしてそれが不可逆性を生み出している、という話をしました。そこでは、最後にエントロピーという用語を引き合いに 出しましたが、正確に定義はしませんでした。そこで、ここで改めて微視的視点からエントロピーを定義します。
ある系において、微視的状態数の多い巨視的状態の方が、微視的状態数の少ない巨視的状態よりもエン トロピーは大きい。
以下に、エントロピーとは何か、と問われたとき、それを言葉で表現するときによく使われるものを列記しました。上記の定義でこれらの表現が包括的に理解できたで しょうか。そして、分子が熱運動をしているため、エントロピーの小さい状態から大きい状態へと遷移することは自然に起こり得るが、その逆は起こらない、すなわ ち不可逆であるということもイメージできたでしょうか。
エントロピー 小 エントロピー 大
・微視的状態数が少ない ・微視的状態数が多い
・集中 ・拡散
・分離している ・混ざっている
・偏っている ・平均化・一様化している
・揃っている ・乱雑である
・秩序がある ・無秩序である
・組織的 ・組織の欠如
・少数派 ・特殊 ・多数派 ・一般的
・画一的 ・多様
こうして、微視的レベルでエントロピー増大の法則を述べると、意外と当たり前な法則と思いませんか?しかし、現実の自然現象を目の当たりにしたとき、その微視的状態数の 多 い少ないが常に直感的に分かるわけではありません。また、理論的にも、微視的状態と巨視的状態とを結びつけることは、簡単な例を除いて、そうたやすいことでは あり ません。観測したり、実験で得られるのはあくまでも巨視的状態量ですので、巨視的状態に対してエントロピー増大の法則をイメージできる表現が絶対に必要となりま す。前回、前々回の講義は、そうした意味で、巨視的状態量に着目しながらエントロピー増大の法則を証明したわけですが、今度はあまりに普遍性をもたせたがゆえ に、 具体的なイメージが湧いてこないということになってしまいました。
そこでここからは、エントロピー増大とは、次の3つの現象の組み合わせであると考えてください。この後、この講義で述べられるほとんどの現象は、これで理解でき ると思います。
① 物の拡散 混合も含みます
② 熱の拡散 高温側から低温側へと熱が流れることです
③ 発熱現象 燃焼、摩擦熱、電気製品からの発熱(電熱)など
①は上記の微視的状態数の大小でイメージできるかと思いますが、次節の例題の中で、さらに詳しくみることにします。②については前回触れましたが繰り返し ましょう。

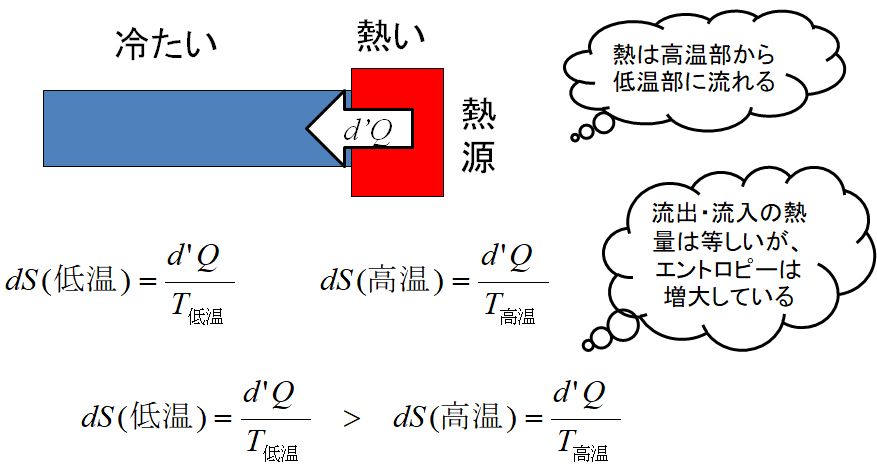
熱は高温部から低温部に流れます。いま高温側の温度を \(T_{高温}\)、低温側の温度を \(T_{低温}\) とし、わずかな熱 \(d'Q\) が流れたとします(\(d’\) は飾り程度に思っておいてください)。熱 は、高温側から出た量と低温側に入った量は同じですが、エントロピーは (熱)/(温度)で定義されていましたから、高温側から出たエントロピーが \(d'Q / T_{高温} \) であるのに対して、低温側に入ってきたエントロピーは \(d'Q / T_{低温} \) となり、分子は同じでも分母が異なるため、後者の方が大きくなります。したがって、温度差があるところを熱が流れるとエントロピーは増大します。 ③も、身の回りいたるところで発熱現象が見られますので、イメージしやすいと思います。そして、発熱すれば、必ず熱の拡散を伴うことになります。 これからの話題では、①、②、③に相当する現象が起こっていたら、エントロピーは増大したと考えてください。
(注) 前回までの抽象的な議論のおかげで、可逆と不可逆もよく分からなくなってしまったという感想が何人かの方からありました。可逆と不可逆は、ある動きを動画撮影し、その映像 を逆回転してみたとき変だなと思えば不可逆ですし、違和感がなければ可逆と思っていただければいいと思います。よく例に出される「覆水盆に返らず」は、コップ から 床にこぼれた水がひとりでにコップに戻る映像はおかしいと思うので、コップから水がこぼれるのは不可逆です。これに対して、もし西から太陽が昇ったとしても、その 映像は見てそれが西からであることを知らなければ違和感はないでしょうから可逆ということになります。振り子の映像も短時間ならば時間を反転しても違和感はな いで しょう。しかし長時間撮影すると、振れはやがて減衰していきますので、それを逆回転で見たら何もせずに次第に振れが大きくなる様子に違和感を抱くことになりますの で、不可逆です。ここで大切なことは、不可逆な現象はエントロピーが増大した証と捉えていただきたいことです。
マクロな視点から見たエントロピーとミクロな視点から見たエントロピーを、第3回の講義で見た気体運動論のように結び付けて理解したいものです。物理学で は前者 は熱力学が、後者は統計力学とよばれる分野が担当するのですが、どちらも見た目まったく異なるような難しい議論が展開され、両者を結び付けて理解するのは一筋縄で はいきません。とはいえ、簡単な例で、その一面をチラ見したいと思い、以下に3つの例題を掲げました。しかし、高校数学Ⅲの領域の数学が使われており、多くの 方に はもはやお手上げかもしれません。しかし、文章を読み、論理の進め方に注目していただきながら、何とか雰囲気だけでも感じ取っていただければ幸いです。流し読みす る上でのポイントを指摘するとすれば、最後の結論と、最後の数式の結果を見て、どれも「対数」で表されていることに気づいていただくことでしょうか。エントロ ピー は対数で定量的には表現されます。エントロピーという概念が普及しない理由の一つが、こうした数学的な難しさにあるんだとい うことを知っていただくだけでも価値があると 思っています。
(1) 例題1.同じ量の気体で、温度が等しく、しかし体積が異なる2つの状態のエントロピー差
体積が \(V_{1}\) と \(V_{2}\)(\(V_{1} < V_{2})\) のときのエントロピー差を計算で求めます。とりあえず、それぞれの体積のときのエントロピーの値を \(S_{1}\)、\(S_{2}\) と表します。
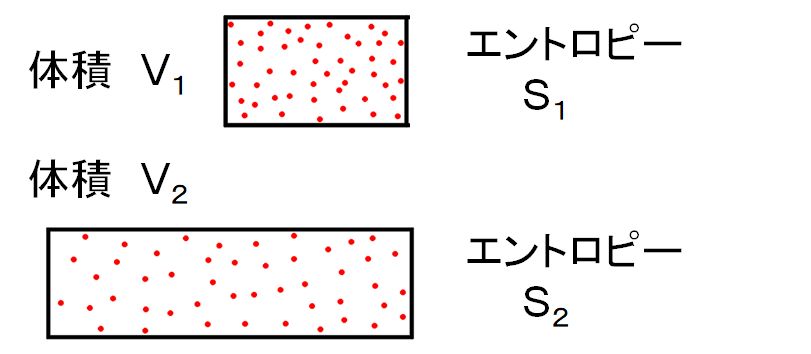
理想気体を考えることにします。理想気体とは、第3回講義資料3.1で述べた気体の状態方程式 \( PV = nRT\) が成り立つ気体をいいます。いま、温度一定のまま、体積を \(V_{1}\) から \(V_{2}\) に膨張させたとします。膨張することで外に向かって仕事をしますから、内部の気体の温度は小さくなる わけですが、温度一定の条件がついていますので、外部から熱を取り入れる必要があります。どれだけの熱を取り入れる必要があるかは、第2回講義資料【参考】仕事の計算例 で述べたように、\(PV\) 曲線の下側の面積を積分で求めることで得られます(図8.3)。すなわち、その熱を \(Q\) とすれば、\( Q=\int_{V_{1}}^{V_{2}} PdV \) となります。ここで、気体の状態方程式 \(PV = nRT\) を使えば \( Q=\int_{V_{1}}^{V_{2}} {\frac{nRT}{V}dV}=nRT \int_{V_{1}}^{V_{2}} \frac{dV}{V}=nRT \log \frac{V_{2}}{V_{1}} \) となります。したがって、異なる体積のエントロピー差は \[S_{2}-S_{1}=\frac{Q}{T} = nR \log \frac{V_{2}}{V_{1}} \tag{1} \] で与えられます。\(V_{1} < V_{2} \) のとき、これは正となりますから \(S_{1} < S_{2} \)、すなわち、同じ温度ならば、体積が大きいときの方が小さいときよりエントロピーは大きくなります。
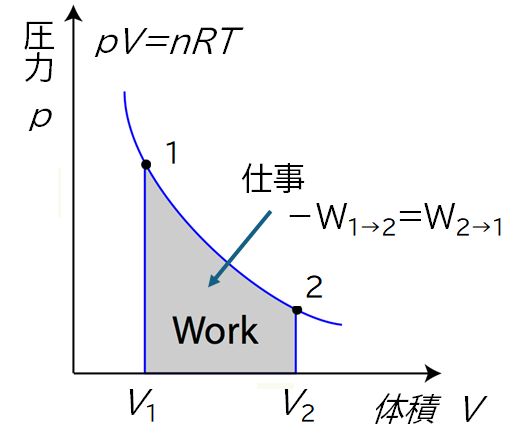
ところで、前にも指摘しましたが、体積を \(V_{1}\) から \( V_{2} \) ( \(V_{1} \lt V_{2} \) )へと変化させる方法にはいろいろあります。図8.4の左右どちらの図も、上段は温度 \(T\)、体積 \( V_{1} \) で、同じ状態ですので、そのエントロピーはともに \( S_{1} \) となります。同様 に、下段も温度 \(T\)、体積 \(V_{2} \)で、そのエントロピーはともに \(S_{2} \) です。しかし、上段から下段の状態に遷移する仕方が異なります。左図では、熱源を接触させ、温度 を一 定に保ちながら、上段から下段へは等温膨張、下段から上段へは等温圧縮という可逆的変化で状態を遷移させています。一方、右図では、上段では、箱の右側が真空で、 その境を取り払うことで左の気体を自由膨張させ、下段の状態へと遷移させています。このとき、外部とは断熱状態ですし、気体は仕事をしないため、体積が膨張し ても 温度は一定のままです。また、下段の状態から上段の状態へとその状態遷移の仕方を反転することで達成することができませんので、不可逆な状態遷移ということになり ます。
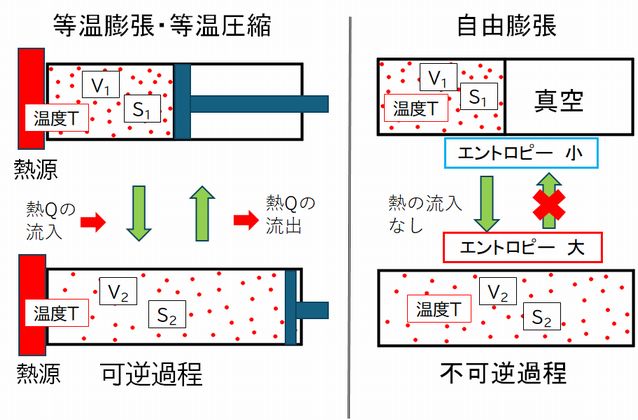
ところで、エントロピーの計算は、可逆変化をしたときにのみ定義されますので、左の図から求めることになり、それが上で述べた計算です。一方、右の図では 不可逆 過程ですので、ここからはエントロピーを計算することができません。しかしあくまで計算することができないというだけで、結果としては左右同じエントロピー変化が あったということです。
(2) 例題2:混合のエントロピー
2種類の理想気体とみなせる気体1(図8.5青色)と 気体2(図8.5赤色)が間仕切りで分離された断熱容器の中に閉じ込められています。体積はそれぞれ \( V_{1} \)、\( V_{2} \) で、同じ温度 \(T\)、同じ圧力 \(P\) にあるとします(始状態)。
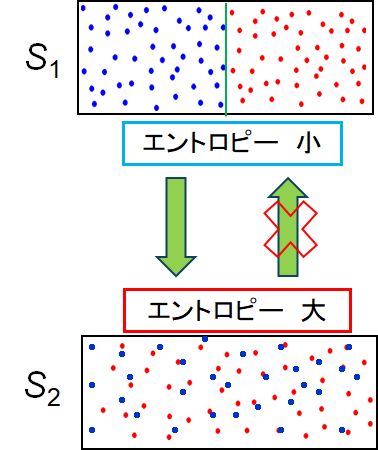
(イ) 間仕切りを取り除くと、2種類の理想気体は均一に混じりあい、平衡状態に達します(終状態)。このとき、温度 \(T\)、圧力 \(P\) はそのままで、体積は \(V=V_{1}+V_{2} \) となります。 この現象はもちろん不可逆過程です。系は外部と熱や仕事の交換をまったくしていませんが、エントロピー変化は起こります。断熱容器の中で理想気体とみなせる2 種類 の気体を混合するときのエントロピー変化を混合エントロピーといいますが、上で述べたように、このままではエントロピーを計算することができません。そこで、次の ような理論的考察から求めます。かなり難解かと思いますが、これも、物理学という学問の論理展開をチラ見していただこうという思いで掲載しました。
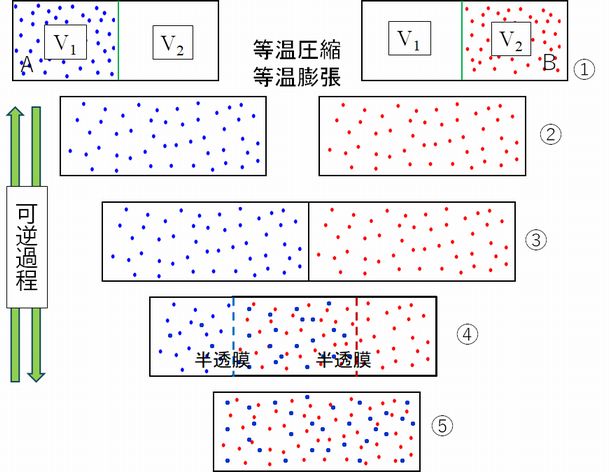
(ロ) 計算を可能にするためには、始状態と終状態とを結びつける可逆過程を見つける必要があります。そこで考え出されたのが半透膜を使う次のような2種類の気体の混 合方法です。 可逆過程ですから、逆過程として混合した2種類の気体を分離する方法が含まれている必要があります。
なお、こうした頭の中だけで描き出した実験は思考実験とよばれますが、物理学が最も得意とするアプローチの一つです。 まず、始状態にある気体をそれぞれ別々の異なる容器の中で断熱自由膨張によって体積を \(V_{1}+V_{2} = V \) にすることを考えます(図8.6 ①→②)。この過程そのものは不可逆ですが、上記例題1で見たように、可逆過程を想定し、①と②のエントロピー差は計算することができます。 次に、2つの容器を接触させます(図8.6 ③)。ここで、その接触部分の壁が半透膜でできていると考えます。ただし、左側の容器の接触面の半透膜は、青色の気体1は全 く通さないが赤色の気体2は自由に通すのに対して、右側の容器の接触面の半透膜は、赤色の気体2は全く通さないが青色の気体1は自由に通すとします。そして、 2つ の容器を互いに入れ子状態に押し込んでゆくと、容器の重なった部分には両方の気体が入ります(図8.6 ④)。重なりが完全になるまでゆっくり押し込むと、体積 \(V_{1}+V_{2} \) の中で2種類の気体も完全に混合されます(図8.6 ⑤ 終状態)。この過程は、⑤から②へと可逆的に戻すこともできます。したがって、このような半透膜を利用した気体の混合過程をすべて準静的な過程とみなすことができ、② ⇄ ⑤のエントロピー変化を計算することが可能となるのです。
(ハ) それではエントロピーを計算してみます。 まず、図5の①と②のエントロピー差は、例題1よりそれぞれ次のようになります。
\[ S_{②}^{A}-S_{①}^{A} = n_{1}R \log \frac{V_{1}+V_{2}}{V_{1}} S_{②}^{B}-S_{①}^{B} =n_{2}R \log \frac{V_{1}+V_{2}}{V_{2}} \]
半透膜を押し込む③→⑤の準静的断熱過程では、各々の気体についてみると何事も起こっていませんのでエントロピー変化は 0 となります。結局、図5の始状態と終状態のエントロピー \(S_{1}\) と \(S_{2}\) の差は、上記の個別に計算した始状態と終状態とのエントロピー差の和となり、
\[ S_{2}-S_{1} =
S_{②}^{A}-S_{①}^{A}+S_{②}^{B}-S_{①}^{B} = n_{1}R \log
\frac{V_{1}+V_{2}}{V_{1}} + n_{2}R \log \frac{V_{1}+V_{2}}{V_{2}} \]
\[ = n_{1}R \log \frac{V}{V_{1}} + n_{2}R \log \frac{V}{V_{2}}
\tag{2} \]
と求まります。右辺は正の値となりますので、\(S_{1} \lt S_{2} \)、すなわち、分離しているときより混合したときの方がエントロピーが大きいという結果が導かれました。
エントロピーはもともと熱の移動に着目して定義された物理量でした。ところが、ここでは、「熱の移動が全くないような状況においてもエントロピーが変化(増大) することがある」ことを示唆しています。また、そうした場合には、熱の移動を考慮した可逆過程を想定して、エントロピーを求める必要があることも確認できた と思います
(3) 例題3:同じ量の気体で、体積が等しく、しかし温度が異なる2つの状態のエントロピー差
熱容量 \(C\)、温度 \(T_{1}\) の個体の温度を \(T_{2} \) まで上昇させたとします。このとき、温度を \(dT\) だけ上昇させるのに必要な熱量 \(dQ\) は \(dQ = CdT \) で与えられます。また、そのときのエントロピーの増加 \(dS\) は、\(dS = \frac{dQ}{T} \) ですので、温度を \(T_{1} \) から \(T_{2} \) まで上昇させたときのエントロピー変化 \(S_{2} - S_{1} \) は次式で与えられます。
\[ S_{2}-S_{1} = \int_{T_{1}}^{T_{2}}dS = \int_{T_{1}}^{T_{2}} \frac{dQ}{T} = \int_{T_{1}}^{T_{2}} \frac{CdT}{T} = C \log ( \frac{T_{2}}{T_{1}} ) \tag{3} \]
\(T_{1} \lt T_{2} \) のとき、これは正となりますから \(S_{1} \lt S_{2} \)、すなわち、温度が高い方がエントロピーは大きくなります。
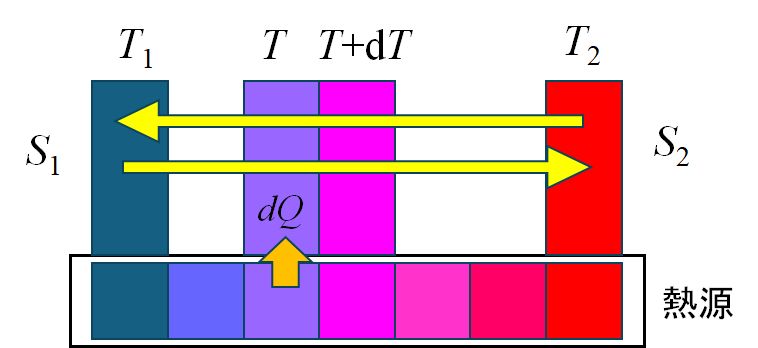
(注) ある系の温度が高いときと低いときとでは、前者の方が後者よりもエントロピーが高い状態と言えます。温度が高い方が分子は活発に動きまわり、その微視的状態数(分子の運動 状態の場合の数も含む)が大きくなるからです。一方、その系に同じ量の熱が流入したとき、あるいは同じ量の熱が流出したとき、その系のエントロピー変化は、 (熱)/(温度)ですので、温度の高いときの方が小さく、温度の低い方が大きくなります。すなわち、同じ熱の量でも、その系に与える影響が異なります。同じ1 万円でも、金をもっている人と、持っていない人ではその影響が異なる、そんなイメージで捉えていただけばいいかと思います。
子供たちがよくする質問に、地球には空気があるのに月にはなぜ空気がないの?というのがあります。答えは、月は地球より小さいために重力が弱く、空気の分 子を捕 らえておくことができず、宇宙空間に逃げていってしまったからです。それでは、地球ではなぜ空気の分子は積もらないの?という質問にはどう答えますか。地球の 重力 に空気の分子が引っ張られているならば、われわれのように、空気の分子も全て地面にへばりついていてもいいはずです。しかし、上空にも、希薄になりますが、空気の分子は存 在します。関連 した質問に、どうして上空ほど空気は薄いの?とか、どうして山の上にいくほど太陽に近くなるのに寒いの?というのもあります。
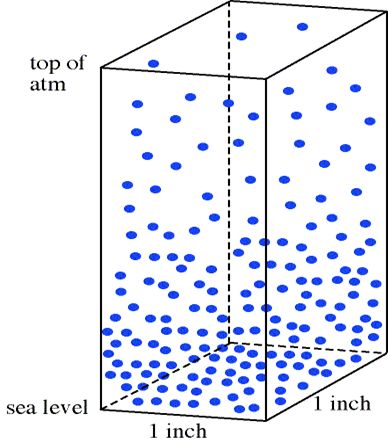
この問いは次の質問とも関連があります。物質の3様態、固体、液体、気体において、もっともエントロピーが大きいのは気体という状態です。だとしたら、どうし て、この世の中のものはエントロピー増大の法則にしたがってすべて気体にならないの?と質問したくなります。物質の3様態が温度に依存することは前にお話しし ましたが、これまでのエントロピー増大の法則とどう折り合いをつけて説明できるかが問題となるわけです。
これらに共通することは、エントロピーだけを考えても、物資の状態は決まらないということです。空気の分子に関して言えば、空気が地面に積もらないのは、分子が 熱運動しているからです(第3回講義)。しかし一方で、空気の分子の運動は重力による制約も受けています。ボールを上に投げれば、ボールは重力により次第に減 速し、速度 0 となったところで突然落下に転じます。したがって、空気の分子も、地面に近いほど速度は大きく、上空に行くほど遅くなります。それが上空ほど温度が低い 理由の一つとなります(大気の水分を含んだ対流、太陽光の影響もあるので、実際にはかなり複雑な側面もあります)。また、速い分子もあれば、遅い分子もありま すから、上空まで行く分子は限られ、上空での空気の分子の量は少なくなります。
物質の3様態についていえば、すでに第3回講義でお話ししたように、分子の熱運動の大きさが温度によって異なり、分子間の相互作用が、その運動をどの程度 束縛す るかによって、固体、液体、気体という状態を呈することになります。結局、地球と空気の分子、分子と分子の相互作用を考える必要があるということです。
それでは、それをどのように定量的に評価したらいいのでしょうか。ここは、いきなり天下り的にそのための評価式を示すことにします。それは、等温等積の条件では、\( F = U - TS \) で定義されるヘルムホルツの自由エネルギー \(F\) が、また、等温等圧の条件では、\(G = H -TS \) で定義されるギブスの自由エネルギー \(G\) がそれぞれ最小となる状態が実現される、というものです。ここで、\(U\) は内部エネルギーとよばれ、分子間などの相互作用を表す項であり、\(T\) と \(S\) はそれぞれ温度とエントロピーです。また、\(H\) はエンタルピーとよばれ、\(H = U + PV\) で定義されます。内部エネルギーだけでなく、系の体積変化も考慮されたエネルギー項です。以下で見るように、この式は、\(U\) または \(H\) が小さくなることが系の秩序をより高める方向に作用し、\(S\) が大きくなり、結果として \(-TS\) が小さくなることが系をよりランダムにする方向に作用するため、両者の拮抗によって、\(F\) または \(G\) の最小の状態が決まることを意味しています。
2種類の自由エネルギーがありますが、普段の生活では、ある温度、ある大気圧のもとでどのような状態が実現されるのかに興味がありますので、等温等圧条件 での自由エネルギー \(G\) について考えることにします。\(G\) は2つの項 \(H\) と \(-TS\) からなりますから、 \(H\) をできるだけ小さくし、 \(- T S \) をできるだけ小さくする(\(T\) および \(S\) はともに正の値ですので、与えられた \(T\) に対して、\(S\) をできるだけ大きくする)ことがその目的には叶うのですが、\(H\) と \(S\) は 独立には決められず、しかも、\(H\) を小さくすれば \(S\) が小さくなり、結果として \(-TS\) が大きくなり、\(S\) を大きくすると(\(-TS\) を小さくすると) \(U\) は大きくなるというように \(G\) への寄与が相反する変化をするため、\(G\) を小さく するためにはその兼ね合いが重要となってきます。
もう少し具体的な例で見ていきましょう。いま、ある物質(たとえば、水)の3態、固体、液体、気体(氷、水、水蒸気)の自由エネルギーを \(G_{固体}\)、\(G_{液体}\)、\(G_{気体}\)、エンタルピーを \(H_{固体}\)、\(H_{液体}\)、\(H_{気体}\)、エントロピーを \(S_{固体}\)、\(S_{液体}\)、\(S_{気体}\) とします。すなわち、
\[G_{固体}=H_{固体}-TS_{固体}、 G_{液体}=H_{液体}-TS_{液体}、 G_{気体}=H_{気体}-TS_{気体} \]
となります。
ここで、エンタルピーとエントロピーはすべて、温度に依存しない定数とします。すると、自由エネルギー \(G\) はどれも、温度 \(T\) の一次関数となり、横軸に \(T\)、縦軸に \(G\) をとれば、それぞれ直線で表されます。このとき、エンタルピーは縦軸の切片となり、 \(H_{固体} \lt H_{液体} \lt H_{気体}\) が成り立ち、エントロピーは直線の傾きに相当し、 \(-S_{固体} \gt -S_{液体} \gt -S_{気体}\) が成り立ち、図8.9のようになります。
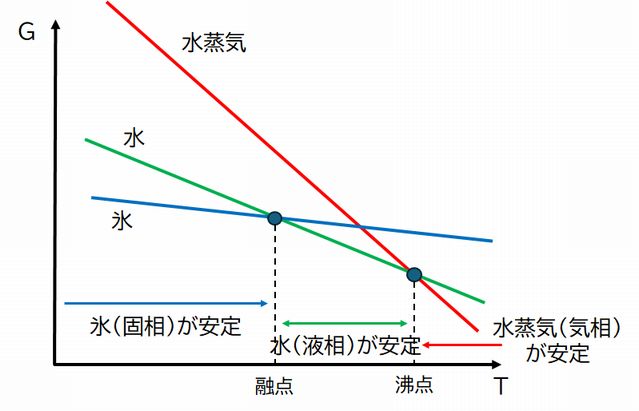
こうして、さまざまな温度における物質の3態それぞれの自由エネルギー \(G\) が与えられたわけですが、ある温度に注目したとき、もっとも \(G\) が小さい状態がその温度で実現される、というのが上で述べたことでした。低温においては、固体(氷)の自由エネルギー(青の直線)がもっと小さく、ある温度(融点)で液体 (水)の自由エネルギーの直線(緑)と交差し、それより高温では液体の自由エネルギーがもっとも小さく、さらに高温で、今度は液体の自由エネルギーの直線と気 体(水蒸気)の自由エネルギー の直線が交差し(交差点は沸点)、それより高温では気体の自由エネルギーがもっとも小さくなります。こうして物質は、低温から高温へと温度を変化させると、固 体(氷)⇒ 液体(水)⇒ 気体(水蒸気)へとその状態を変化させることになる、と説明されます。
地球を取り巻く空気についても、エントロピー的には一様に広がろうとします。一方、地球と空気の分子の相互作用は、両者をくっつけようとしま す。そのせめぎあいの中で、自由エネルギーがもっとも低くなるのが、現在の空気の分布の仕方、ということになるわけです。
ところで、水蒸気が水となるとき、\(H\) (エンタルピー)は減少し、エントロピー \(S\) も減少します。しかし、エンタルピーが減少した分が熱として外部に放出され(凝縮熱)、外部のエントロピーは増大します。また、 氷が水となるとき、エントロピーが増大し、エンタルピーも増大します。しかし、外部から熱が流入することで外部のエントロピーは減少します。こ のよう に、エ ントロピーの局所的な減少は起こることは覚えておいてください。しかし、エントロピーがどこかで減少した以上に、かならずどこかでそれ以上のエント ロピーが生み出されており、トータルでは必ず増大している、それがエントロピー増大の法則です。
