
バネとゴムはどちらも引っ張れば伸び、手を離すと縮みます。しかし、実は、両者の伸び縮みの物理的なメカニズムは本質的に異なっています。
バネはエネルギー弾性とよばれ、バネを構成する原子間に働く相互作用エネルギーが最も低い状態へ復帰しようとして生じる弾性です。第2回講義の原子間のポテン シャルエネルギーで説明しましたように、原子と原子には最適な距離があり、何もなければその距離(自然長)を保っています。しかし、外から力を加えて引っ張る と、 その距離が長くなります。そして力をかけるのをやめるとその最適距離へと戻るという仕組みです。これがバネの伸縮の原理です。
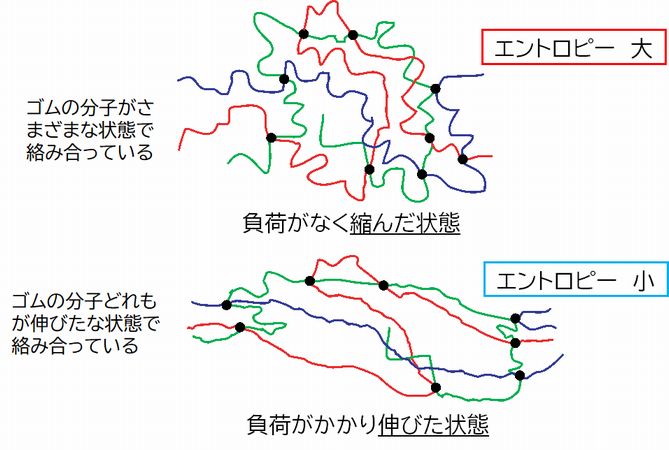
これに対して、ゴムの弾性はエントロピー弾性とよばれ、エントロピーが最大になろうとして(物質の取り得る微視的状態数がより多い状態になろうとして)生じる弾性と説明 されます。
ゴムは多数の高分子鎖(紐状の分子)が複雑に絡まったような構造をしています。高分子鎖はさまざまな形をとることができます。そうした高分子鎖の集団の長さ(要 するにゴムの長さ)という巨視的量でみると、伸びた状態を構成するためには多くの高分子鎖が伸びた状態をとる必要があり、そのためにはゴムを引っ張ってあげる 必要 があります。しかしそれが自然状態で起こる確率は小さいため、引っ張るのをやめると、各高分子鎖は縮み、巨視的量としての長さも短くなります。ところで、なぜ各高 分子鎖が縮むかというと、高分子鎖を構成する原子が運動しているからであり、バネのときのように、縮むことがエネルギー的に安定であるからというわけではあり ませ ん。


ゴム弾性の仕組みを説明する幼稚園生モデルです。
上図右では、幼稚園生が両手を繋いで列を作っています(ゴムを構成する高分子鎖の一つに相当します)。一方の端の子は固定されたポールにつかまっています。もう一方の端 の子 は先生と手を繋いでいます。幼稚園生たちは常に自由気ままに動き回っているとします(分子を構成する原子の熱運動に相当します)。先生がこの幼稚園生たちをきれいに横一 列に 並べようとすれば、相当の力をもって引っ張る必要があります(ゴムを伸ばすことに相当します)。もし、並べたとしても、先生は幼稚園生たちから強く引っ張られるこ とになるでしょう。それは、幼稚園生の列の形に何か安定な形があるからではなく、とにかく彼らが勝手に動きまわれば列の形は様々に変化し、ポールと先生との距 離と いう巨視的な量でみれば、直線的に並んだ距離よりも短い距離になる確率が圧倒的に高いということに過ぎないわけです。幼稚園生たちのランダムな動きが、先生をポー ルに近づける力となるわけです。
もちろん、このモデルでは、先生は単にポールに近づくだけでなく、振り回されるでしょう。しかし、鉄が伸び縮みしないのと同じ論理で、ゴムの場合にも、高分子鎖の 数の膨大さによって、ある平均値の長さに留まり、見た目の長さが変動することはありません。