図2.1.さまざまなエネルギーとその可換性を示す例
エントロピーは、物理学では、熱力学および統計力学という分野で導入される物理量です。その熱力学には、根幹をなす2つの法則があります。
熱力学第1法則 エネルギー保存の法則
熱力学第2法則 エントロピー増大の法則
この講義の目的は、第2法則を理解していただくことなのですが、そのためにはまず第1法則を理解していただくことが必要となります。第1法則は、正確 にはわからないとしても、ちょっとした説明で直感的に受け入れられるものだと思いますので、数行の文章で完結してしまうのですが、これからの話を理解していただくために 知っておいていただきたい具体的な内容がいくつかありますので、今回はこの第1法則について解説します。 なお、数式がたくさん出てきます。理解を深めるためには非常に有効だと思いますが、数式の意味がわからないからといって今後の話についていけなくなるというものでもあり ません。説明文だけでもある程度は理解できると思いますのでご安心ください。
まずは、エネルギーとは何か、から始めようと思いますが、「ある系が他に対して仕事をする能力をもつとき、その能力をエネルギーという」などと定義されま す。 ここで、「系」はシステムの訳語で、自然科学では頻繁に使いますので、覚えてください。次に「仕事」もれっきとした物理用語ですが、これについては、たとえば「対象と する系と外部との間でやりとりされる力学的なエネルギー」などと辞典には書かれています。これでは堂々巡りとなり、結局は、エネルギーも仕事も定義されたこと になっていません。基本的な用語というものは得てしてこうしたもので、まあ漠然と、ふだんエネルギーというものに対してもっているイメージでスタートし、これ から述べるいくつかのコメントを通して理解を深めていただければ十分です。
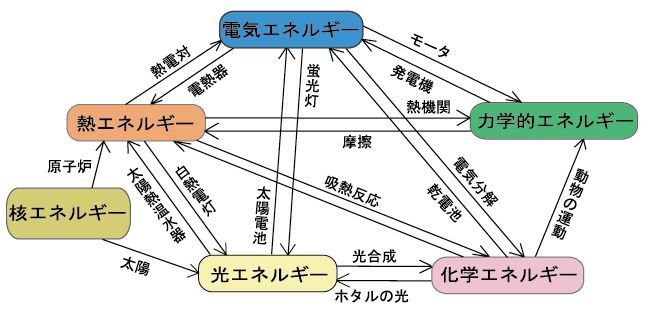
エネルギーに関してこれからの講義でポイントとなる点、すなわち熱力学第1法則であるエネルギー保存の法則をまとめると、次のように表現されます。 「エネ ルギーにはさまざまな形があります。それらは相互に変換可能であり、変換によってその量が変化することはありません。すなわち、エネルギーの量は常に保存され ます。」これが今回の講義で述べたいことのすべてです。特に違和感なく受け入れていただけたでしょうか。しかし、これを深読みすると、この講義のテーマ、エン トロピーに関する重要なポイントが隠されています。それについては追々お話しすることにします。ここではとりあえずさまざまなエネルギーの形と、それらが相互 に可換である ことを示した図2.1を見て、このまとめの文章の意味を確認してください。なお、エネルギーの分類の仕方は人によって多少違いますので、本によって表現は異なるか もしれません。

図2.1.さまざまなエネルギーとその可換性を示す例
例を上げましょう。標高の高いところにあるダムの水は、高いところにあるというだけで位置のエネルギー(ポテンシャルエネルギー)をもっています。そし て、より低いところにある発電所まで落下させることで、その位置のエネルギーは水の運動エネルギーへと変換され、水の運動エネルギーは発電機が回る 運動エネルギーへと変換され、さらに電気のエネルギーへと変換されます。火力発電や原子力発電では、石油、天然ガス、石炭、放射性物資などの物質がもつエネルギー (化学エネルギー)を、熱エネルギーを介して水蒸気の大きな運動エネルギーに変換し、それが発電機が回る運動エネルギーへ変換され、電気エネルギーとなりま す。 その過程では、あちらこちらで発電には直接結びつかない熱も大量に発生しますが、それらも含めると、エネルギーの量は決して増えも減りもしません。 さらに、電気のエネルギーは家庭に届くと、たとえば照明として光のエネルギーへと変化されます。そしてその光のエネルギーはどこへ行ってしまったのかというと、最 終的には、光があたった壁や家具などを温め、熱のエネルギーとなります。やはり、エネルギーは決して消失することはありません。その量は増えも減りもすること なく、ただただ姿を変えていくだけ、ということです。
?? であるとするならば、なぜ、エネルギーを節約しようというのでしょうか?皆さんはどのように 考 えますか?これに対する答えも、エントロピー増大の法則から導かれます。第4回の講義でその話題になります。それまで、しばらく自分なりに考えてみてください。
エネルギーのいろいろな形態を紹介しようと思います。この後の講義でいろいろな具体例をあげて説明する上で、ここで登場した式を 知っているとより理解が深まるだろうというものを中心に取り上げています。ちょっとした物理の講義になりますが、単なる公式集程度に思っていただければそれでよく、理解し ないと後の話につい ていけないというものでもありません。後で具体例が出てきたときに、数学が分かる人はここに戻って確認していただければいいかなと思います。
(1) ポテンシャルエネルギー(位置エネルギー)Potential energy
物体に対して重力やバネによる外力が働いているとき、その力に逆らう方向に物体を移動させるためにはエネルギーが必要です。そこで、このときのエネルギーを (力)×(移動距離) で定義し、「仕事」とよびます。式で表すと、ある物体に力 \(F\) がかかっているとき、その物体を力に逆らう方 向に距離 \(x\) だけ移動させるには \(Fx\) のエネルギーが必要である、となります。 重力に逆らって質量 \(m\) の物体を高さ \(h\) だけ持ち上げるとき、重力は \(mg\) で与えられますので(\(g\) を重力加速度といいます)、 必要なエネルギーは \(mgh\) となります。バネの場合には、力の大きさはバネの縮んだ長さ(あるいは伸びた長さ)\(x\) に比例しますので、すなわち、力がバネの変化量 \(x\) に依存して変わるため積分で表され、\( \int_{0}^{y} kx \, dx = \frac{1}{2} ky^{2} \) となります。ここで \(k\) はバネ定数、\(y\) は最終的なバネの縮んだ(あるいは伸びた)長さです。
 ところで、力が加えられ、エネルギーを使って物体の位置やバネの長さが変化したわけですが、その仕事のエネルギーはどこにいったのでしょうか。エネルギー保存の法則に従え
ば、何らかのエネルギーに変換されたはずです。そこで、その高い位置にいることや、バネが縮んでいること(あるいは伸びていること)自身がエネルギーをもった
状態であると考え、これを位置エネルギーとよびます。英語では、潜在的に保有しているエネルギーと
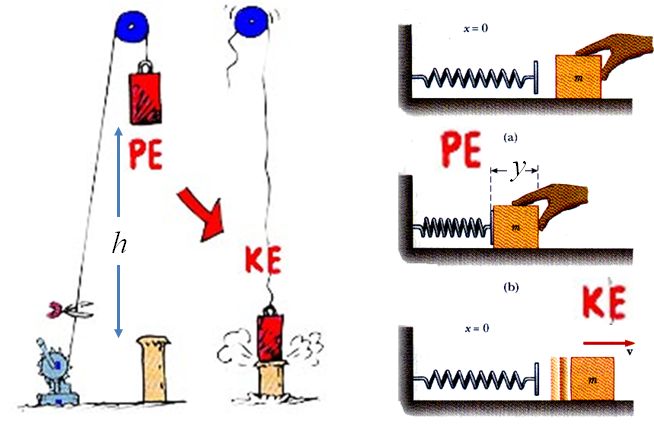
いう意味でポテンシャルエネルギーとよびます。実際、図2.2に示したように、高いところにあるものは落下することで仕事をすることができますし、バネは縮んだ
状態から伸びることで(あるいは伸びた状態から縮むことで)、やはり仕事をすることができます。
ところで、力が加えられ、エネルギーを使って物体の位置やバネの長さが変化したわけですが、その仕事のエネルギーはどこにいったのでしょうか。エネルギー保存の法則に従え
ば、何らかのエネルギーに変換されたはずです。そこで、その高い位置にいることや、バネが縮んでいること(あるいは伸びていること)自身がエネルギーをもった
状態であると考え、これを位置エネルギーとよびます。英語では、潜在的に保有しているエネルギーと
いう意味でポテンシャルエネルギーとよびます。実際、図2.2に示したように、高いところにあるものは落下することで仕事をすることができますし、バネは縮んだ
状態から伸びることで(あるいは伸びた状態から縮むことで)、やはり仕事をすることができます。
図2.2 ポテンシャルエネルギー(PE)が
運動エネルギー(KE)に変換される
(2) 運動エネルギー Kinetic energy
質量 \(m\) の物体が速度 \(v\) で運動しているときの運動エネルギーは \( \frac{1}{2} mv^{2} \) となります。質量が同じならば、速度の二乗に比例して運動エネルギーは大きくなるということで、これはこのまま覚えておいてください。
運動エネルギーの導出に興味のある方は こ ちら をご覧ください。
(3) 熱 Heat
熱は、より熱い系(物体)からより冷たい系(物体)へ自発的に伝達されるエネルギーとして定義されます。熱は、あくまでもエネルギーの移動の形式であり、 系の中にこれだけ存在すると定義できる物理量ではありません。一方、内部エネルギーという用語もあり、これは、系を構成する分子の運動エネルギーや分子間の相 互作用エネル ギーなどの総和で、系のエネルギー状態を示す量となります。 外部から熱が入ると内部エネルギーが増えます。しかし、同じ内部エネルギーの増加を熱でなくとも引き起こすことができるため、系の内部エネルギーのうちどの部分が 「熱」に由来するといった区別をすることができません。そこで、熱は系の状態を示す量とはなり得ないのです。ただ、実際には、内部エネルギーと熱を混同して記 述することがしばしばあります。 ちなみに、普段「熱がある」という表現は、その物体の温度を意味していることが多く、この「温度」はその系の状態を示す量となります。それでは温度とは何かが問題となりま すが、それは次回の講義のテーマとなります。また、熱と温度の違いは、第3回の講義以降、より明確に区別されながら議論されることになります。
(4) 仕事 Work
すでに(1)で述べましたが。対象とする系と外部との間でやりとりされる力学的なエネルギーを 仕事 とよびます。後に、ピストンというシステムが出てきますが、 ピストンを押し込むことはピストンに対して外部から仕事をすると表現します。一方、ピストンの内部の気体が膨張してピストンが押し出されるときは、ピストンが外 部に対して仕事をするといいます。
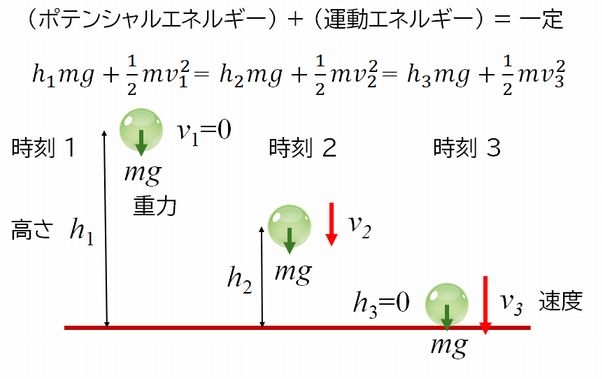
位置エネルギーと運動エネルギーの和が保存されることを使うと、次のような問題を解くことができます。
下図で示したように、質量 \(m\) の球を床からの高さ \(h_{1}\) から落下させます。このとき、速度 \(v_{1}=0\) です。球が高さ \(h_{2}\)、\(h_{3}\,(= 0)\) に達したときの速度 \(v_{2}\)、\(v_{3}\) を求めなさい。ただし、\(g\) は重力加速度です。
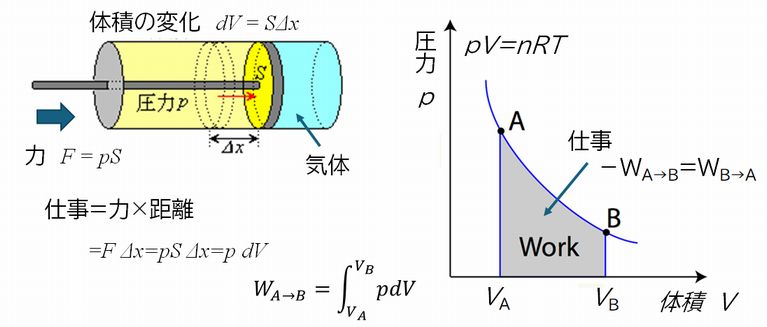
ピストンを押し込むときの「仕事」について考えてみましょう。
ピストンは、断面積 \(S\)
のシリンダーに気体を封じ込めたまま、外力によって滑らかに押し込んだり、気体の膨張により押し出されたりします。気体の圧力が \(p\)
のとき、圧力は単位面積当たりの力として定義されますので、ピストンにかかる力 \(F\) は \(F=pS\)
となります。いま、ピストンが軸方向に \(\Delta x\) だけわずかに動いたとします。このときの仕事は、(力)×(距離)
で与えられますから \(F\Delta x = pS \Delta x = p \, dV\) となります。ここで \(dV=S\Delta
x\) は、変化した気体の体積にあたります。
ところで、圧力 \(p\) は気体の体積 \(V\) に依存します。すなわち、\(V\) の関数で、理想気体では、
\(p=nRT/V\) と表されます。ここで、\(n\) は気体の量(モル数)、\(R\) は気体定数、\(T\)
は温度で、ここでは定数とみなします。すると、体積が \(V_{A}\) から \(V_{B}\) に変化したときの仕事 \(W_{A\to
B}\) は以下のような積分で求められます。
\[W_{A\to B}=\int_{V_{A}}^{V_{B}} p \, dV=\int_{V_{A}}^{V_{B}}
\frac{nRT}{V} dV=nRT \, (\log \, V_{B}-\log \, V_{A}) =nRT \log
\frac{V_{B}}{V_{A}} \]
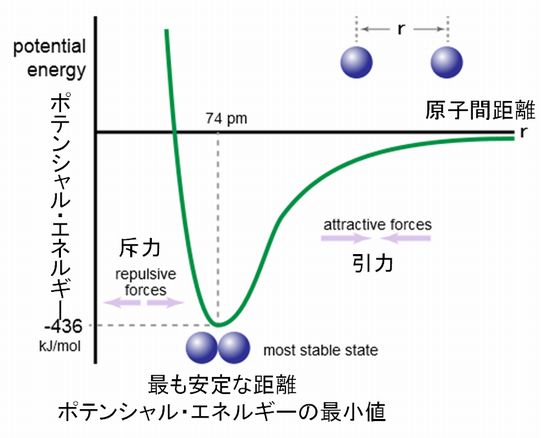
2個の原子間に働く相互作用のポテンシャルエネルギーは、両者の距離の関数として以下の図のように表されます。無限に離れたときをゼロとしています。 グラフの最小値を与える距離が最も安定な距離であり、それより近づくと互いに反発して斥力がはたらき、遠のくと、近づくように引力がはたらきます。
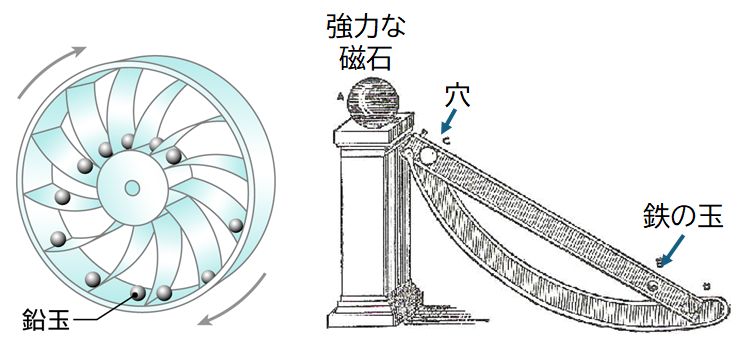
エネルギー保存則は、エネルギーを使わずしてエネルギーを生み出すことはできない、すなわち無から有は生じないことも意味しています。しかし、古くから、 そ うした夢の機関(これを永久機関と言います;機関とは力学的エネルギーを生み出すよう設計された機械で、エンジンの日本語訳です)を 作れないか考えられてきました。中には、巧妙な説明によって、簡単にはそのトリックを見破れないものもありますが、エネルギー保存則を基礎におけば、たとえトリックを見破 れなくとも、原理的にそれが不可能であることから 、一刀両断に、そうした発明はフェイクだと切り捨てることができます。図2.3に示したのは、そんな永久機関だと主張された例です。
戦後、ショーウインドウなどでよく見かけた玩具に水飲み鳥(平和鳥)があります。いまではすっかり見なくなってしまいましたが、一見永久機関のような振舞 いをするため、永久機関の話題のときにはよく引き合いに出されるスター的存在です。YouTubeに動画がありますので、知らない方はぜひ見てみてください。 この 講義で は、今回だけでなく、何度も登場します。この水飲み鳥の動作原理をエントロピーの視点から説明できるようになれば、この講義の内容をかなり理解したと言えるくらい、重要 な位置づけをもった玩具なのです。

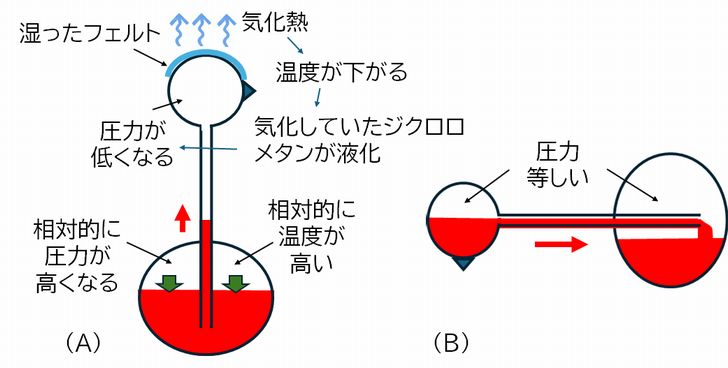
水飲み鳥の動作を説明します。 水飲み鳥と水のはいったコップを用意します。水飲み鳥の構造は、2つのガラスの球(頭部と腹部)を首に見立てた管でつないだ形をしています。首の中央付近に支点が 設定してあり、頭部と腹部の間を内部の液体が移動することで重心が移動し、前後に揺れ動きます。頭部はフェルトで覆われており(図の黒い部分)、コップの水に 頭が触れたとき、頭部が濡れるようにしてあります。内部には気化しやすい液体としてジクロロメタンなどがはいっており、目立つように青色(赤色のものもある) に着色され ています。
まずは人の手で頭部をコップの水の中に押し込み、フェルトを濡らします。手を離せば、腹部に液体のジクロロメタンがありますので、その重みによって頭を上
げた姿勢をとり、しばらくは慣性で前後に揺れ動きます。このとき、頭部と首、そして腹部の上部は、何も見えませんが、気化したジクロロメタンで満たされていま
す。
しばらくすると、濡れた頭部から水が気化することで頭部の温度が下がり、気化していたジクロロメタンが液化し、頭部・首の部分の気圧が下がります。一方、腹
部 の気化した部分は温度・圧力ともに変わりませんので、腹部の液面を押し下げ、管内の液面を頭部に向かって押し上げるように働きます(① ②およびA)。
これまで腹部の方が重かったのですが、液体が移動したことで支点より頭部側のモーメントが大きくなり、身体が前に傾き、くちばしがコップの水の中に浸かりま
す。このとき、頭部を覆うフェルトが再び濡れることになります(③)。
ところで、ここまでは、気体のある領域は頭部と腹部にあり、液体で分断されていました。しかし前に倒れたことで、首に相当する管が水平になったとき、別々で
あった首の部分の気体領域と腹部の気体領域が一つに合体し(④およびB)、液体は腹部へと一気に還流します(⑤)。重心が再び腹部へと移り、水飲み鳥は勢いよ
く起き上が り、しばらくまたゆらゆらと揺れます。これが延々と繰り返されるため、永久機関のように見えるわけです。
水飲み鳥の動作原理の理解は、この説明で特に問題はないように思えます。しかし、そもそもこの水飲み鳥の運動のエネルギー源は何なのでしょうか?エネル ギー保存の法則が成り立つかぎり、エネルギーの供給なしには運動が継続されることはありません。さて、何でしょうか?考えてみてください。答えは、第5回にお 話ししようと思います。
水飲み鳥については、この講義を受けるにつれ、さまざまな疑問がまた湧きあがってくることと思います。そして、その都度、それを理解す ることで、この玩具のもつ奥深さに感心することになると思います。
⇒ 第3回 熱運動