エントロピーは、自然科学ではもちろんのこと、社会科学においてもしばしば出会う重要な物理量です。たとえば、環境問題やエネルギー問題を論じるとき、 「エントロピー増大の法則」に基づいた議論が展開されます。また、自然科学のなかでも、生命とは何か、といった一見、物理学とは異なる分野における問題を扱う ときにも、 生命系の自己組織化する能力や進化が、エントロピー増大の法則と本質的に相容れないように見えるため、古くから議論がなされてきました。しかし、そうした重要 性にもかかわらず、多くの人にとっては、名前すら知らない、知っていてもよくわからないというのが普通ではないでしょうか。それはひとえに、その概念の難しさ に 起因しています。そのため、教える側にとっても、習う側にとっても悩ましい物理量となっています。 たとえば、対となるエネルギーという物理量が比較的直感的に捉えやすいのに対して、エントロピーは、数式を使わないと説明し難い部分があって、言葉だけの説明では、なかな かその本質が見えてきません。実際、熱力学や統計力学というエントロピーを扱う専門分野の教科書はもちろんのこと、啓蒙書といえども、正確を期そうとして数式 が並び、しかも難解な 説明が多いため、理解するのに四苦八苦することになります。
そこで本講義では、正確さは多少犠牲にして、エントロピーを感覚的に、あるいは直感的に捉えられるような解説を試みよ うと思います。また、数式の使用もできるだけ抑えようと思います(とは言っても、結構出てきます。しかも、多くの方には馴染みが薄い対数が主役となります)。私 がこれまでに行った文系学生を対象とした講義経験では、四則演算しかない単純な文字式でも、それが出てきただけで話を聞くことに拒否反応を示す人が結構いて、 具体的な数値で説明してほしいと いう要望もありました。文字式の方が一般論が展開でき、数値をもっての説明は特殊な一例を示したに過ぎませんから、自然科学としては邪道であることは明らかで すが、要望を受け入れ、できるだけ両方の表現を併記するよう努力してきました。これからの資料のなかには、文字式と数値例が混在したものがありますが、そうし た背景があって行っていることと了解しておいてください。
この講義は、あくまでも、非専門の履修者の皆さんにエントロピーの概念を理解していただくためのものです。エントロピーが醸し出す風景を遠くから眺めても ら うことを意図したもの です。エントロピーを本格的に理解したいと思って履修した方には不満が残るであろうことは重々承知していますが、この点はぜひご了解ください。もしこの 講義で興味が湧いてきた折には、必ず専門書を開き、正確な議論を確認していただきたいと思います。しかしそうした場合でも、ここで得たエントロピーに関するイ メージは役立つものと思っています。
また、この講義を履修した方の中には、単に自然科学の科目を受けてみたいと言う人も結構おられると思います。そうした方に対しては、自然科学的な知識を提 供するだけでな く、社会科学とは違う、自然科学独特の思考法や論理の進め方に触れる機会を提供することも意味あることと思っています。そのような点にも注意しながら解説してい きたいと思っています。たとえば、第6回、第7回の講義でカルノーサイクルという話題を取り上げました。多くの啓蒙書では省略することが多い内容かと思いま す。それを敢えて取り上げたのは、難しい数学はまったくなく、しかし自然科学における独特の証明法が使われているので紹介したいと思ったからです。また、特に 後半は、ほとんど数学を使わず、論理的な議論を楽しむような内容になっています。前半は比較的数式が多くて数学が苦手の人にとっては苦しい展開かと思います が、 後半を期待していてください。
エントロピーについて語るとき、「エントロピー増大の法則」が常にその中心的な教義となります。この法則によれば、この世界では、物事に変化が起これば必 ずエントロピー が増大します。したがって、必ず過去よりも未来の方がエントロピーが大きくなっています。1927年に英国の天文学者アーサー・エディントンが、過去から未来 へと流れる時間の一方向性を表現するのに「時間の矢」という言葉を使いましたが、エントロピー増大は、まさにその時間の矢を示す指標ということになります。こ のことがなぜ問題かといいますと、次のような事情によります。
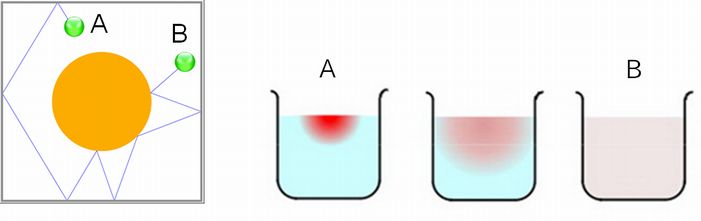
図1.1左は、ビリヤードでの緑のボールの軌跡を描いたものです。中央の橙色の円は固定されています。AとBどちらから打った結果、AとBのどちらに到達 したかわかりますか?わかりませんよね。物理学的にはどちらでも起こり得るからです。一方、図1.1右は、水に赤インクが落ち、水全体に拡散した状況を描いた ものです。AからBに時間が推移した か、BからAに時間が推移したか、わかりますよね。すなわち、図1.1左は可逆な現象、図1.1右は不可逆な現象を示しています。そしてこの図1.1右こそ、 エントロピー増大の法則によって説明される現象であり、不可逆性がエントロピー増大の法則の重要な帰結の一つとなります。すなわち、物理学では、図1.1左の ような可逆な現象を記述する 学問体系と、図1.1右のような不可逆現象を記述する学問体系が共存しており、両者の間には矛盾を抱えているのですが、それぞれの内部では矛盾なく体系が構築 さ れてお り、それが奇妙な状況を作り出しています。そうした意味でも、エントロピーは本質的に理解の難しさを内包している物理量だともいえるのです。

可逆と不可逆の問題には次のような側面もあります。ニュートンの運動の法則に則って物体や天体や分子の運動を記述する学問体系を古典力学といいます が、ここではすべての現象は可逆的に記述されます。可逆的とは、ある時刻 \(t=a\) にある状態Aにあったものが、別の時刻 \(t=b\) に異なった状態Bに変化したとしたとき、単に時間を反転すれば、また、同じ法則にしたがって状態Aに戻ることを意味しています。このことは、状態 Aと状態Bが見た目異なった様態を示していたとしても、与えられた運動の法則の下では、どちらからどちらへも推移できるわけですから、2つの状態がもつ情報量は等しいこと を意味しています。と なると、われわれがふだん感じている時間とともに進化するとか、進歩するという概念は、可逆な世界では単なる錯覚ということになります。見た目が変わっても、 それらがもつ情報量は変わらないといっているわけですから。それに対して不可逆な世界では、過去から未来に向けてエントロピーは必ず増大すると言っているわけ ですから、進化とか、進歩という概念は本質的に存在し得ることになります。
ところが、話はそう単純ではありません。ここで新たな問題が生じます。エントロピーが増大するとは、と調べると、秩序あるものはより無秩序になり、ランダ ム さを増すこととあります。進化や進歩とはまったく真逆なことが書かれているのです。これはどう理解したらいいのでしょうか?これについて考えるのが、この講義 でもっともやりたいことの一つなのです。
環境問題でもエントロピー増大の法則はしばしば取り上げられます。空気汚染や水質汚染などの環境汚染問題、都市におけるゴミ・廃熱問題などでエントロピー 増大の法則が非常にネガティブなものとして顔を出します。秩序あるものが無秩序になることがエントロピー増大であると言われれば、どう考えてもわれわれにとっ て歓迎すべき法則ではなさそうです。
日本で「公害」が社会問題化したのは1960年代でしょうか。ほぼ同じ時期、1972年、ローマクラブ第一報告書『成長の限界』が発刊され、現在のまま人 口増加や 環境破壊が続け ば、資源が枯渇し(あと20年で石油が枯渇すると推定された)、人類の成長は限界に達すると警鐘が鳴らされました。それに対して経済学者ガルブレイスは 、 1975年、「成長の限界は資源の枯渇よりも廃棄物の捨て場の枯渇によって決まる」と述べています。ここで「廃棄物」は「エントロピー」に置き換えてもよく、 エントロ ピー増大の法則が人類を破滅に導くかもしれないという警告でもありました。実際、『人間の終焉』(1976) など、終末論的な科学論もこの頃ちょっとしたブームになりま した。
しかし同じ頃、エントロピーにもっとポジティブな側面があることもわかってきたのです。1977年にノーベル化学賞を受賞したイリヤ・プリゴジンの著した 『混沌からの秩序』(1979)の前書きから引用しましょう。
われわれの科学の遺産の中に、今日まで答えられたことのない2つの基本的疑問が残っている。その1つは無秩序と秩序の関係である。有名なエントロピー増大の法則は、世界は 秩序から無秩序へと進化していると述べているが、一方、生物進化や社会の進化は単純なものから複雑なものが生じることを示している。これはどうして可能なの か?どうしたら無秩序から構造が生じるのか?この疑問に対しては大きな進歩があった。今では、物質とエネルギーの流れという非平衡が秩序の源泉となりうること がわかっている。 (中略) 秩序と無秩序とは複雑な概念である。力学の静的記述を行う構成単位と、エントロピー増大によって表現された進化のパラダイムを達成するために導入されなければ ならない構成単位とは別物である。この移行は「活性ある」物質という物質の新概念を生み出す。活性ある物質と呼ぶのは、物質が不可逆過程を生み、不可逆過程が 物質を組織化するからである。
これだけでは何を言いたいのかよく分からないと思いますが、現時点では解説はやめておきます。ただし、混沌から秩序が生まれることを説明するための大きなパラダイム変換が 起こったことを暗示している、そんな風に理解していただければとりあえず十分かと思います。ちょっと逆説的な表現を使えば、混沌を生み出す力(エントロピー増 大の法則)こそ秩序を生み出す原動力である、とでも言えるでしょう。そして、これを理解していただきたいことこそ、この講義が目指すところなのです。
エントロピーは、物理学のなかでは、熱力学と統計力学の2つの分野で論じられます。熱力学では温度とか、熱とか、体積などマクロな量を用いてエントロピー が論じられます。これに対して統計力学では、膨大な数の分子からなるシステムを考え、それらの運動を統計学的に解析して、ミクロな視点から論じられます。同じ 物理 量であるにもかかわらず、視点を変えるとかなり異なった姿をわれわれに見せてくれます。こうしたマクロな視点とミクロな視点から同じ物事を考えるというのは社 会科学においてもよくあることと思いますが、自然科学での取り扱い方を見ていただくのもこの講義の目的の一つです。
エントロピーは情報という概念と密接に関係しています。実際、情報理論という工学の分野では「情報のエントロピー」が定義されており、数学的な形式は物理 学のエント ロピーとまったく同じ形式で定義されています。物理学のエントロピーと情報理論のエントロピーが同じものなのか、単に形式的に同じだけでまったく別概念である のかがよく議論されます。しかし、2010年、中央大学と東京大学の研究チームが情報をエネルギーに変換することに成功し、両者が同じ概念に基づいていること が示されました。上で述べたエントロピーと進化や自己組織化などを論じるときなどにも、情報という視点は重要な意味合いをもってきます。
この他、現在の流行語の一つ、ダイバーシティ(多様性)についても、エントロピーという観点から見てみることも面白いと思っています。
以上、漠然とした話でしたが、エントロピーになぜ関心が向けられるのかについて、いくつかの視点を紹介しました。自然科学にしろ、社会科学にしろ、エント ロピーについて 理解を深めることは非常に役立つことと思います。しかし難敵ですので、それなりの覚悟をしておいてください。何とか最後までお付き合いいただけることを願って います。