これまでのエントロピーに関する議論から少し大風呂敷を広げ、エントロピー増大を多様性を創出するメカニズムと捉え、そこにマックスウェルの悪魔に匹敵す る何らかの選択機構が作用することで自己組織化が達成されるという話題をいくつか取り上げようと思います。
生物集団だけでなく、一般に、系の内部で絶えまなく起こる構成要素の変異の発生もエントロピーを増大させる重要な機構の一つです。典型的な例として、生物の進化に関する ダーウィン・モデルを見てみましょ う。
ある生物種の集団を考えます。その集団内には常にある頻度でDNAに突然変異が生じます。変異が起こる要因としては、物理的要因、化学的要因、生物的要因と いろいろありますが、すべてDNAという分子に起こった偶発的な出来事であり、何らかの意図や方向性をもったものではありません。エントロピー増大の典型的な 現象といえます。そしてこれが、個体差を生み出し、集団内に多様性をもたらします。この個体差には、環境への適応度において差を生み出すものが存在します。肉 食 動物に追われる草食動物は逃げ足の速さによって生存率が変わるでしょう。足の速さは追いかける肉食動物にとっても生存率に影響を与える形質です。そうした環境 への適応度の高い形質を発現する遺伝子は、それをもつ個体の生存率をあげ、その遺伝子を引き継いだ子孫はそれをもたない子孫よりも集団のなかで多数派となって い くことでしょう。このメカニズムが進化における「自然選択」とよばれるものです。しかし選択を行う実体がいるわけではありません。「生存」という生物の本質的 な属性が「選択」とよぶような機構を生み出しています。マックスウェルの悪魔は、選択する実体が想定された思考実験でしたが、現実の現象では、そうした選択す る実体をもたない、構成員間の相互作用によって生じる選択機構がむしろ一般的でしょう。
結局、進化は、ランダムな変異の発生というエントロピー増大の機構と、自然選択とよばれる選択機構との組み合わせによって起こる現象と捉えることができま す。
自然科学とは異なる分野の例を取り上げてみます。これは物理学的な意味でのエントロピーではなく、情報のエントロピーに関わることです。
対象は自然言語です。若い人を中心に絶えず新語や新しい言い回しが生まれています。また、格言などが、本来の意味とは異なる意味で使われているということもよく話題にな り ます。それは、自然言語の体系の変化を目論んだというよりは、ほとんど偶発的に思いつきで生まれたり、何とはなしに広まり、定着していったりしたものです。若 い人が日本語を汚しているとよく年寄りに避難されますが、生物の進化と同様、変異が生まれるのは不可避であ り、実際には、そうした変異の発生によって言語体系が崩れるといったことはそう簡単には起きそうにありません。それは、これも生物進化と同様、従来からある単語であろう と、新語であ ろう と、みな選択にさらされるからです。われわれは話したり、文章を書くとき、聞き手に自分の思いを的確に伝えるという言語の目的にそって多くの単語の中から選択作業を 行います。そうして、ある単語は高い使用頻度をもち、またある単語はやがて忘れ去られ死語となっていきます。また、間違った使い方であろうと、相手に自分の言 いたいことが伝わったのであれば、それで言語としての役割は果たしているわけです。
ここで自然言語を取り上げたのには訳があります。実は、単語の使用頻度について興味深い法則が成り立っていることが知られているのです。
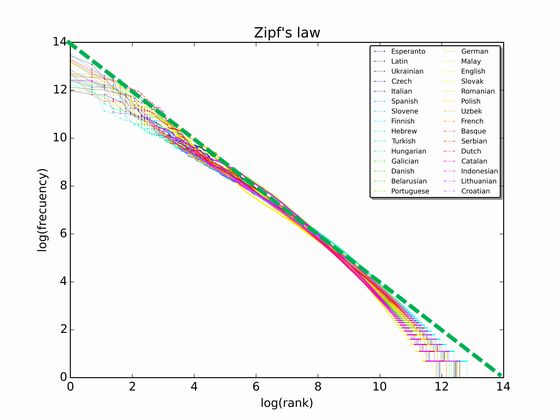
図12.1に示したのは、ウィキペディアの中の文章について、単語の使用頻度を調べ、使用頻度の多い順に並べ、その使用頻度をプロットしたものです。横軸に単語を 使用頻度の高い順に並べたときの順位、縦軸にそれぞれの単語の使用頻度をそれぞれ対数目盛でプロットしています。複数、色のついた線があるのは、さまざまな言 語のデータを表しているからです。破線は傾き−1 の直線です。すべてがほぼ傾き −1 の直線に近くなります。これは、ウィキペディアだけではなく、任意の本をもっ てきて調べても似たような結果が得られます。この事実を最初に発見した人の名前にちなみ、これをジップ(Zipf)の法則と言います。

このように、横軸に順位、縦軸にその頻度や何らかの値を両対数グラフでプロットしたとき直線となる事例は他でも見られます。順位に沿ってプロットしていますから、右下 がりになるのは当然ですが、曲線ではなく、直線になる場合が多々あり、何らかの自己組織化が行われている可能性を示唆しているため、興味がもたれています。た だし、傾きは必ずしも −1 とは限 らないため、広くべき乗分布の法則といいます(注)。この他にも、たとえば日本の各都市の人口、小売り業界各社の売上げなどを、順位を横軸に、その値を縦軸にプロット すると、べき乗分布を示すことが知られています。
(注)\( y = a x^{b} \) の \(b\) をべき乗とよびます。両辺の対数をとると \( \log y = \log a + b \log x \) となります。\( \log y\) を縦軸、\( \log x \) を横軸にグラフを描くと、直線となります。ジップの法則では、\( b=-1\) となっています。
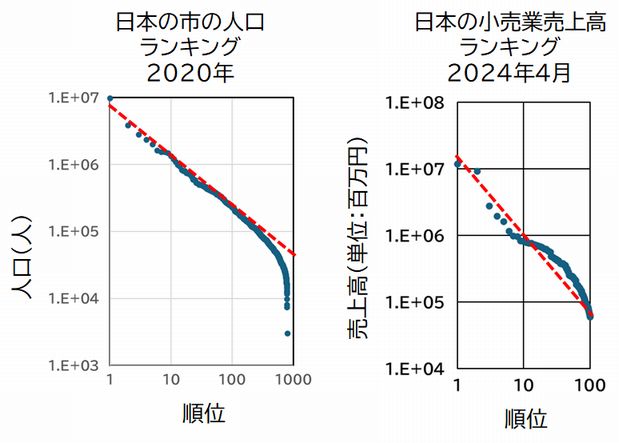
こうした例をみると、変異の発生や新たな構成要素の侵入、そして選択機構があって、捨て去られるものがあるという構図を描くことができます。都市の人口分布 では絶えず人は生まれ、死んでいきます。そして人々はどの町に住もうか選択をします。企業も絶えず新しい会社が起業され、互いに競争し、そして廃業・倒産する 会社もあります。これらは、前々回述べた非平衡開放系として捉えれば、誕生や起業は流入に、死や廃業・倒産は流出に相当し、同時にその内部で何らかの選択機構 が働いているシステムと捉えることができます。選択機構に関していえば、進化と同様、選択する主体がいるわけではなく、そのシステムの機構として、あるいは構 成要素間の相互作用の結果として何らかの選択が行われていると解釈されます。そうして、その結果として、べき乗分布という秩序が知らず知らずのうちに実現され ているのです。
ところで、直線の傾きに何か意味があるのでしょうか。たとえば、ジップの法則の −1 という傾きはどのようなメカニズムで達成されるのでしょうか。残念ながら現 時点ではまだよくわかっていません。しかし、もし傾きがもう少し緩やかであったら、それは、高順位のものと低順位のものとの間の格差が小さくなり、よりエントロ ピーが高い状態となります。単語の使用頻度でいえば、多くの単語が同じような頻度で使われることを意味し、聞く側にとっては、知らない単語もかなりの頻度で使 われるため理解するのが難しくなるでしょう。一方、傾きが急になれば、きわめて偏った単語の使い方を意味し、今度はよりエントロピーの小さな状態となります。 聞く側にとっては、今度は知っている単語ばかりで分かりやすいかもしれませんが、意外性に欠け、つまらないでしょうし、話す側にすれば、伝えたい内容が十分に 表現できない不満が残るかもしれません。そのちょうどいい加減が−1の傾きということなのですが、なぜこの値かは説明が難しいというわけです。
傾きが緩やかであることは、小売業の売上でいえば、どの会社も似たような業績ということですし、人口の分布でいえば、全国どの市町村の人口も似たようなものと いう状況となります。一方、傾きが急になると、小売業の売上は少数の大企業の寡占状態ですし、人口の分布でいえば、都市への一極集中を意味します。そうした両 極端の中間となるような分布に自然と落ち着いていくことをべき乗分布のデータは示しています。エントロピーの言葉でいえば、自由エネルギー最小の状態で説明し たような、エントロピーを増大させようとする力と、あるところに集中させようとする力が釣り合い、何らかの量が最適となる状態があることを示唆しています。
ここでもう一つ、こうしたシステムがもつべき重要な特性が浮かび上がってきます。それは、変異や新たな侵入者を受け入れる能力です。それなりに出来上がってい るシステムにとって、系を乱すことになるかもしれない変異を受け入れるということはそう容易ではないはずです。人工物である機械を思い浮かべてみてください。 変異とは要するに故障が生じることですから、変異は直ちにシステム・ダウンへと結びつきます。それは、コンピュータのように高度に組織化された精密機械であれ ば あるほど、すなわち多くの部品からなり、それらの部品間の相互作用が厳密に決まっていればいるほど、小さな変異でもシステム崩壊をもたらします。自然言語と異なり、コン ピュータ言語は、ちょっとしたプログラムミスが大規模なシステムダウンを引き起こすことがあります。これに対して 生命系をはじめとする上記で掲げたようなシステムでは、多くの場合、そうした変異を受け入れることができるのです。
どうしたら、そうした寛容性をもったシステムを構築することが可能なのでしょうか。
あまりにも厳密に組織化された系、要素間の相互作用が非常に強い系では、変異を受け入れる寛容性は生まれないでしょう。人工物の機械がまさにこれにあたりま す。結晶などもそうです。不純物が混じると融点の低下などを引き起こし、安定性が損なわれます。一方、あまりにも相互作用が弱く、要素がどれもほとんどランダ ムに動いているような系では、変異は容易に受け入れられ、系に与える影響もほとんどないでしょうが、そもそも組織化されていないということかもしれません。と なると、ちょうどいい相互作用というものがありそうです。完全にランダムでもなく、かといって予測可能なほどには決定論的ではない中間の状態、そうした感じで しょうか。
多様性の創出(エントロピー増大)と選択機構のセットが自己組織化を引き起こす一つの重要な要素となることがわかりました。しかしそうだとしても、徹底して選 択機構が働くことで最終的に最適値へとたどり着き、そこで状態の変化は終焉を迎えることにならないのでしょうか。しかし、実際には、最適値にたどり着くことは まず ありません。一つには、内部で変異が生まれるのは不可避だからです。しかしそれでも、変異の発生を徹底的に抑え込む方向にシステムを構築することも可能だった かもしれません。
たとえば、進化は自然選択によって環境に適したものが選ばれることで起こったと語られます。そして単純な生物から複雑・高等な種が誕生した過程が進化だと考え られてきました。そうであるとするならば、なぜ選ばれた数百種類くらいの種でこの地球生態系が構成される状況にならないのでしょうか。また、同じ種の中でも強 く選択圧がかかるならば、なぜもっと均一な個体の集団とならないのでしょうか。
さまざまな生物のDNAの研究が進み、化石だけに頼っていた進化学も大きく変わってきました。ダーウィン以来、変異は自然選択によって集団に広まったり、排除 されたりするというどちらかというと決定論的な視点で進化が論じられてきました。ところが、1960年代の終わり、日本の遺伝学者である木村資生が進化の 中立説を提唱、その後進化学のなかで確たる学説として定着しました。それによると、変異のなかには、自然選択という観点からは中立であり、すなわち適応度が高 いとか、低いとか判断できないようなものが圧倒的に多く、それが集団に広まる(といっても感染するものではなく、何世代も経た後、その変異を受け継いだ子孫が 集 団の中で多数いる)かどうかは確率的であるというものでした。これはダーウィンの進化論を否定したものではなく、進化の新たな側面を明らかにしたものと捉えら れています。言うなれば、進化は、適者生存による単純なものの複雑化・高等化の過程という側面だけでなく、多様性を生む機構という側面があることが示されたの です。何千万といわれる生物種を生み出してきたことも進化の重要な側面であるというのです。進化もまた決定論と確率論の境界にあるといえるでしょう。
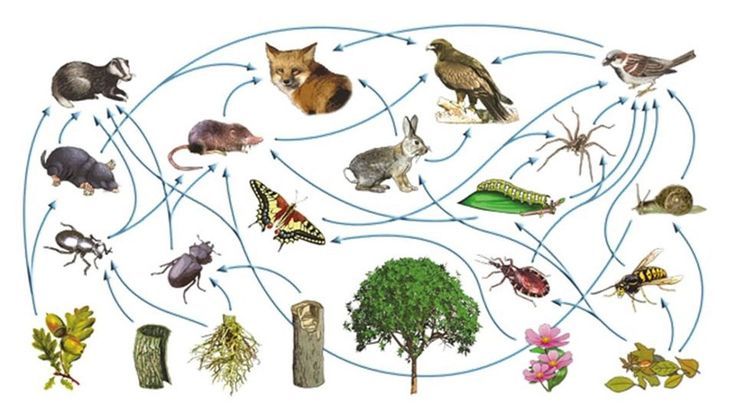
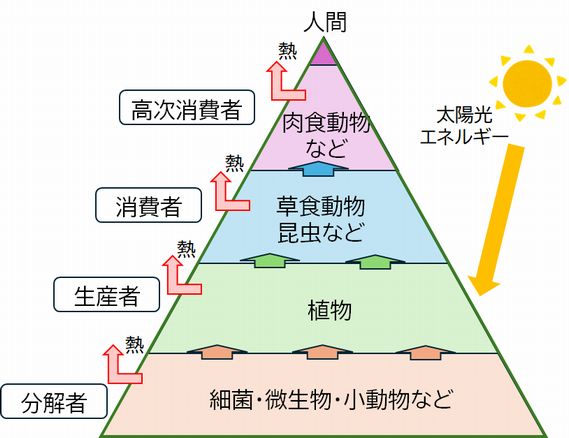
生物多様性を守ろうと叫ばれています。でもなぜそうしなければならないのでしょうか。種の絶滅が起こるということが環境破壊の指標となるので、実は環境問題に 主眼があって、それを別の視点から注意喚起しているとか、まだわれわれが解明していない生物資源が失われてしまうことへの危惧であるとか、かつて存在した生物 種への郷愁であるとか、いろいろな解釈がありますが、本質はどこにあるのでしょうか。環境省のホームページには次のように書かれています。「生物多様性とは、 生きものたちの豊かな個性とつながりのこと。地球上の生きものは40億年という長い歴史の中で、さまざまな環境に適応して進化し、3,000万種ともいわれる 多様な生きものが生まれました。これらの生命は一つひとつに個性があり、全て直接に、間接的に支えあって生きています」。すなわち、地球生態系という複雑なシ ステムのなかで、多様な生物が行う多様な相互作用(たとえば食物連鎖;図12.3)によって生み出される創発的な人類への恩恵、それこそが生物多様性保全の本 質だと言 いたいのだ思うのですが、これまで話してきたように、生物多様性に限らず、個と集団の関係性が重要である複雑系とよばれるシステムの意義や仕組みが十分理解で きていない現状では、どうしても漠然と、多様性は大切だよ、という以上のメッセージが出せないでいるように思います。
多様性を保持することの意義について、一つだけ重要なキーワードをあげておきます。それは冗長性です。冗長性という用語は情報関係で使われることが多いのです が、多様性を考える上でも重要な概念の一つなのです。情報関係では、コンピュータシステムにおいて、耐障害性を高めるためにネットワークを含むシステム全体を 二重化して、予備システムを準備することを冗長化といい、冗長化によってシステムの信頼性、安全性を確保した状態を冗長性があると表現します。本来一つあれば い いシステムをもう一つ作り、万が一に備えるわけで、そのもう一つのシステムが余分であり、障害さえなければ無くてもいいものという意味で冗長だというわけで す。
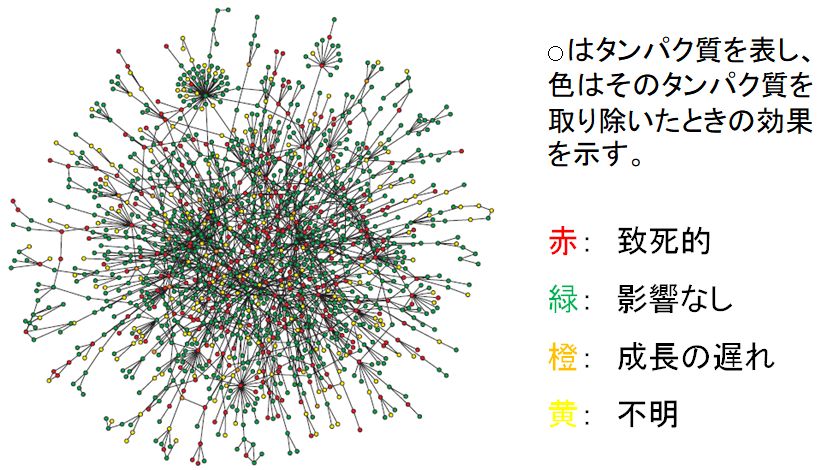
ところで、図12.4は、酵母菌に含まれるタンパク質の相互作用ネットワークを示したものです。一つ一つの丸がタンパク質を、そしてそれらを結ぶ線が、そ れらタ ンパ ク質間に相互作用があることを表しています。色が付いていますが、赤は、そのタンパク質がないと致死的な状況となったことを意味し、それに対して緑は、そのタ ンパク質が1つなくても特に致死的状況には陥らなかったものを示しています。すなわち、無くてもいいタンパク質です。したがって、そのタンパク質無しでシステ ムを構築してもよかったわけで、このシステムは冗長にできているということになります。しかもたくさんのそうしたタンパク質があることがわかります。もちろ ん、緑で示したタンパク質が複数欠失したらどうなるかは保証できません。
こんな虫食いの文章があるとします。「関東▢方は平野部では晴れ▢でしょう。19日より▢差しの出る時間は▢くなりそうです。空▢の乾燥に加 え▢、風が強まる▢め、火の取□扱いには十分▢注意下さい。」虫食い部分はほとんどが復元できたと思います。ということは、復元できた▢の部分は無くてもいい ということになり ます。したがって自然言語体系も、実は冗長性をもったシステムであることがわかります。
ここで重要な点の一つは、最初にあげたコンピュータシステムの例では、余分なシステムが明確に特定できます。それに対して、酵母菌のタンパク 質相互作用システ ムでも、自然言語でも、たまたまある要素が欠落しても機能しますよ、というだけで、その欠落した要素が余分だと特定できたわけではありません。すなわち、シス テムがもつ冗長性がより複雑な構造に依存して醸し出されてくるということです。漠然とした表現になりますが、多様性をもつ要素が互いに関係性をもちながらネッ トワークを構成することで、どこかに障害が起こっても、残りの部分でそれを補償できる、そうしたシステムとなっているということかと思います。
冗長性の意義を示すもう一つの例をあげましょう。
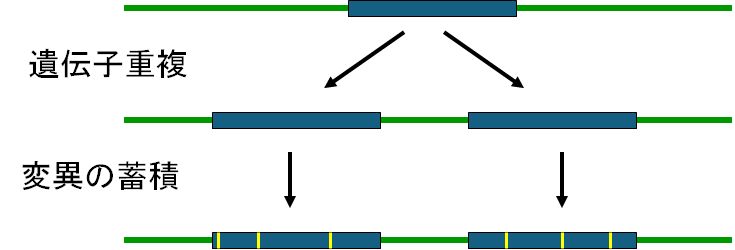
進化の過程で、遺伝子を含むDNA上のある領域が重複して複製されることがあります。これを遺伝子重複といいますが、実際、われわれのDNAを調べてみると多 くの遺伝子が複数存在しています。それらは、重複して複製されたときはまったく同じでも、進化の過程で変異を起こし、少しずつ機能が変化していきます。たとえ ば、赤血球に含まれるヘモグロビンというタンパク質は(遺伝子はタンパク質の情報をもちます)、肺で酸素を吸着し、末梢の細胞へと酸素を運搬する機能をもちま すが、やはり遺伝子重複によって得られた複数のタイプが存在します。そのうちあるヘモグロビンは胎児のときに働き、あるものは出生後働いています。胎児は母親 の胎盤を通して母親のヘモグロビンから酸素を奪う必要があるため、胎児のヘモグロビンは母親のそれよりも酸素吸着能が高くなっています。こうした機能の微妙な 違いは、遺伝子重複とその後の変異を通して獲得されたものであり、哺乳類誕生のための重要なステップでした。
身近な例では、この他に、われわれの色覚を担う赤色、緑色、青色感受性タンパク質の遺伝子も、もともと単に光に反応するだけのものが遺伝子重複によって数を増や し、変異して対応する色の役割分担が決まってきたものです。味覚や嗅覚も同様にしてさまざまな味や匂いに対応できるようになりました。ちなみに、味覚の中でも 、苦味に反応する苦味受容体遺伝子はヒトでは数十種類ありますし、嗅覚においては800種類程度あります(ただし、ヒトの場合、嗅覚の遺伝子の半分はもはや機 能 していません)。
これまでの話の流れに沿って言い換えると、遺伝子重複が起こったその段階では単に冗長性が増したに過ぎないわけですが、その後の変異によって遺伝子の機能が多 様化し、システムの機能の複雑化、高機能化が達成されたことになります。したがって、冗長性というのは単に同じものが複数あって、互いに代替可能というだけで なく、それらの機能が微妙に異なることで、システムを複雑化・高機能化し、さらには頑健性 robustness を増すことにつながると推定することができます。
われわれは静的な秩序にこそ真理があると思いがちです。数学に代表されるように、それは時を超えて変わることのないものであり、だからこそ重要だと思ってきま した。そして、その対極にカオス状態を考えます。そこでは要素間の相互作用が希薄で、すべての事象が確率的に起こります。それに対して静的な秩序は構成要素間 の 強い相互作用によって達成されます。エントロピーの言葉で表現すれば、静的秩序はきわめてエントロピーの低い状態であり、カオスはエントロピー最大の状態で す。しかしいま、その中間状態に注目が集まっています。それもよりカオスに近い、カオス一歩手前の状態です。それを「カオスの縁」とよんでいます。そしてそこ にこそ進化可能性があり、創造性に最も満ちた状態だと考えられています。絶えず変異が生まれ、一方で消滅していくものがありながら多様性が保持されています。 しかしそれだけだったら単なる烏合の衆ですが、構成要素間の相互作用による何らかの選択機構がそこに加われば、動的な秩序を生み出します。完全にランダムでも な く、完全に決定論的でもない。それはしばしばべき乗分布という形でわれわれにその秩序の一面を垣間見させてくれたりもします。
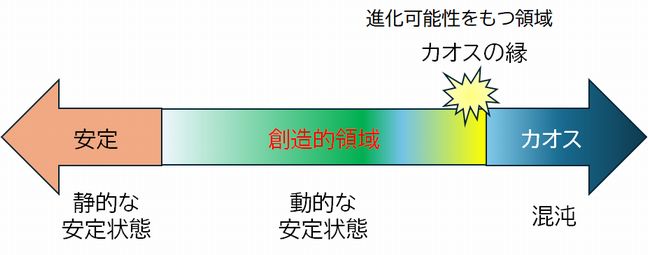
図12.6 ブレークスルーはカオスの縁で起こる
左から、安定領域、創造的領域、カオスの縁、カオス領域
秩序を生み出すということは何らかの最適化機構が働いているからですが、それはすべての可能な状態を見渡したうえでの最大値あるいは最小値で はなく、無数にあ る極大値あるいは極小値の一つにすぎません。したがって、一つの極値に永遠に留まることなく、外部環境の変化、新たな変異の創出による変化に応じて絶えず極値 から極値へと変遷が続きます。しかも、外部環境の変化や新たな変異の創出による内部環境の変化が個々の構成要素に影響し、個々が変化、そして個々の変化がまた 内部環境の変化を誘発するというフィードバック・ループによっても、最適状態の変遷が絶え間なく続きます。絶対的に安定な状態は存在しません。それこそが進化 可能性をもったシステムであり、このダイナミズムこそ “生きている” ことだと言えるのではないでしょうか。結晶構造のような静的で美しい世界、それこそ自然界 の真理であるといった自然の捉え方、それは魅力的に映るかもしれませんが、むしろ死んだ世界の美しさといえるのかもしれません。非平衡開放系において、ほぼ定 常状態を維持しながらも、そこに留まることなく変遷しづける自然界、それこそエントロピー増大が生み出した生きた世界といえるのではないでしょうか。
(注)こうした状況に対して、日本の研究者は、よく、鴨長明の『方丈記』の冒頭の文章を引用します。
行く川のながれは絶えずして、しかも本の水にあらず。よどみに浮ぶうたかたは、かつ消えかつ結びて久しくとゞまることなし。世の中にある人とすみかと、またかくの如し。
エントロピー・多様性・複雑系の講義に最後までお付き合いいただきましてありがとうございました。最初の講義でも述べましたが、エントロピーは難解な概念で、教える側にとって も、聞く側にとっても悩ましいものです。それでもエントロピーは重要な概念であり、社会科学を勉強する人たちの中にわずかであってもそれに興味をもつ人たちが いることを考慮し、その方々のためにという思いでこの講義を起ち上げました。わかりにくい内容が多々あったと思います。ここまでお付き合いいただいた方々には ご苦労様でしたとねぎらいたい気分です。
自然を見る見方が少しは変わったでしょうか。あるいは、こんな視点もあるんだと納得していただけたでしょうか。エントロピーそのものは十分理解できなかった としても、皆さんの中でそうした変化が少しでもあって、いままで学んできた、そしてこれから学ぶ社会科学に対する見方に新たな視点が加わったとすれば幸いで す。